题目内容
18.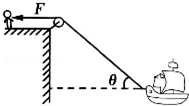 如图所示,人在岸上拉船,已知船的质量为m,水的阻力大小恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力大小恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )| A. | 人拉绳行走的速度为vcosθ | B. | 人拉绳行走的速度为$\frac{v}{cosθ}$ | ||
| C. | 船的加速度为$\frac{F-f}{m}$ | D. | 船的加速度为$\frac{Fcosθ-f}{m}$ |
分析 绳子收缩的速度等于人在岸上的速度,连接船的绳子端点既参与了绳子收缩方向上的运动,又参与了绕定滑轮的摆动.根据船的运动速度,结合平行四边形定则求出人拉绳子的速度,及船的加速度.
解答 解:A、船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度.如右上图所示根据平行四边形定则有,v人=vcosθ.故A正确,B错误.
C、对小船受力分析,如左下图所示,则有Fcosθ-f=ma,因此船的加速度大小为a=$\frac{Fcosθ-f}{m}$,故C错误,D正确;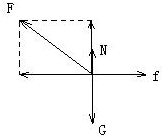
故选:AD.
点评 解决本题的关键知道船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度,并掌握受力分析与理解牛顿第二定律.

练习册系列答案
相关题目
8.关于天然放射性,下列说法正确的是( )
| A. | 所有元素都有可能发生衰变 | |
| B. | 放射性元素的半衰期与外界的温度有关 | |
| C. | 放射性元素与别的元素形成化合物时不再具有放射性 | |
| D. | 一个原子核在一次衰变中不可能同时放出α、β和γ三种射线 |
6. 竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )
竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )
 竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )
竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )| A. | 总可以找到一个v0值,使小球垂直撞击AC段某处 | |
| B. | 总可以找到一个v0值,使小球垂直撞击最低点C | |
| C. | 总可以找到一个v0值,使小球垂直撞击CB段某处 | |
| D. | 无论v0取何值,小球都不可能垂直撞击轨道 |
3. 将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
 将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )| A. | 小球的质量为0.2 kg | |
| B. | 小球受到的阻力(不包括重力)大小为0.20 N | |
| C. | 小球动能与重力势能相等时的高度为$\frac{20}{13}$ m | |
| D. | 小球上升到2 m时,动能与重力势能之差为0.5 J |
10.下列说法正确的是( )
| A. | 一对平衡力所做功之和一定为零 | |
| B. | 一对平衡力所做功之和不一定为零 | |
| C. | 一对作用力与反作用力所做功之和一定为零 | |
| D. | 一对作用力与反作用力所做功之和不一定为零 |
7.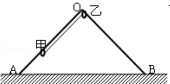 如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )
如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )
 如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )
如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )| A. | 两环整体重心的运动轨迹是以O为圆心,以R=$\frac{L}{2}$为半径的半圆弧 | |
| B. | 小环乙向下运动过程中,小环乙重力的功率一直增大 | |
| C. | 小环甲向上运动过程中,绳子拉力对小环甲先做正功后做负功 | |
| D. | 两环总动能达到最大时,两环的速度大小都是v=$\sqrt{\frac{2-\sqrt{2}}{2}gL}$ |