题目内容
9.有两个完全相同的金属小球A和B,A带电荷3Q,B带电荷-Q,已知它们相距为r时的静电力为F,现将它们互相接触再分开,并使二者距离为2r,求A、B之间的静电力.分析 两个完全相同的金属小球,将它们相互接触再分开,带电量先中和后平分,根据库仑定律即可解题.
解答 解:两个完全相同的金属小球,将它们相互接触再分开,带电量先中和后平分,所以A、B所带的电荷相等都为:$\frac{3Q-Q}{2}$=Q,
根据库仑定律得:
F=k$\frac{3Q•Q}{{r}^{2}}$
而F′=k$\frac{Q•Q}{(2r)^{2}}$
解得:F′=$\frac{1}{12}$ F
答:A、B之间的静电力大小为$\frac{1}{12}$ F.
点评 本题主要考查了库仑定律的直接应用,注意两个完全相同的金属小球,将它们相互接触再分开,带电量先中和后平分,难度不大,属于基础题.

练习册系列答案
相关题目
19. 光滑绝缘水平桌面上平行于桌面的直导线中的电流方向与电子的初速度v0方向相同,如图所示.则下列说法中正确的是( )
光滑绝缘水平桌面上平行于桌面的直导线中的电流方向与电子的初速度v0方向相同,如图所示.则下列说法中正确的是( )
 光滑绝缘水平桌面上平行于桌面的直导线中的电流方向与电子的初速度v0方向相同,如图所示.则下列说法中正确的是( )
光滑绝缘水平桌面上平行于桌面的直导线中的电流方向与电子的初速度v0方向相同,如图所示.则下列说法中正确的是( )| A. | 电子将向右偏转 | B. | 电子将向左偏转 | ||
| C. | 电子将沿直线运动 | D. | 电子的轨道半径将增大 |
20.关于电场强度与电势的关系,下列说法中正确的是( )
| A. | 电场强度相等的各点,电势也一定相等 | |
| B. | 电势为零的位置,场强也一定为零 | |
| C. | 电势高的位置,场强不一定大 | |
| D. | 沿着电场强度的方向,电势逐渐降低 |
17.有关固体和液体,下列说法中正确的是( )
| A. | 固体分为晶体和非晶体,其中所有晶体的光学性质都是各向异性的 | |
| B. | 同种元素组成晶体的物质微粒在空间整齐排列,其“空间点阵”必定相同 | |
| C. | 液晶的物理性质表现出各向异性 | |
| D. | 液体具有流动性是因为液体分子具有固定的平衡位置 |
14.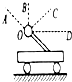 伽利略根据小球在斜面上运动的实验和理想实验,提出了惯性的概念,从而奠定了牛顿力学的基础,早期物理学家关于惯性有下列说法,其中正确的是( )
伽利略根据小球在斜面上运动的实验和理想实验,提出了惯性的概念,从而奠定了牛顿力学的基础,早期物理学家关于惯性有下列说法,其中正确的是( )
 伽利略根据小球在斜面上运动的实验和理想实验,提出了惯性的概念,从而奠定了牛顿力学的基础,早期物理学家关于惯性有下列说法,其中正确的是( )
伽利略根据小球在斜面上运动的实验和理想实验,提出了惯性的概念,从而奠定了牛顿力学的基础,早期物理学家关于惯性有下列说法,其中正确的是( )| A. | 没有力作用,物体只能处于静止状态,因此力是维持物体运动的原因 | |
| B. | 物体抵抗运动状态变化的“本性”是惯性 | |
| C. | 行星在圆周轨道上保持匀速率运动的性质是惯性 | |
| D. | 观察和实验表明,对于任何物体,在受到相同的作用力时,决定它们运动状态变化难易程度的唯一因素就是它们的速度 |
1.关于运动物体的轨迹与所受合外力的关系,下列叙述正确的是( )
| A. | 受恒力作用的物体一定做直线运动 | |
| B. | 做曲线运动的物体一定受变力作用 | |
| C. | 做曲线运动的物体,所受合外力的方向与速度方向成某一夹角 | |
| D. | 受变力作用的物体,一定做曲线运动 |
18.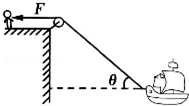 如图所示,人在岸上拉船,已知船的质量为m,水的阻力大小恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力大小恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
 如图所示,人在岸上拉船,已知船的质量为m,水的阻力大小恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力大小恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )| A. | 人拉绳行走的速度为vcosθ | B. | 人拉绳行走的速度为$\frac{v}{cosθ}$ | ||
| C. | 船的加速度为$\frac{F-f}{m}$ | D. | 船的加速度为$\frac{Fcosθ-f}{m}$ |
19.下列说法中正确的是( )
| A. | 一定质量的理想气体经过绝热压缩,气体的温度升高、压强增大 | |
| B. | 浸润现象是由于附着层的液体分子比液体内部稀疏,分子间作用表现为引力造成的 | |
| C. | 在一定温度下,饱和汽的分子数密度是一定的 | |
| D. | 一切自发过程总是沿着熵增加的方向进行 | |
| E. | 能量耗散使能的总量减少,也导致能量品质的降低 |
 真空中有三个点电荷,它们固定在边长50cm的等边三角形的三个顶点上,每个点电荷都是+2×10-6C,求它们所受的库仑力?
真空中有三个点电荷,它们固定在边长50cm的等边三角形的三个顶点上,每个点电荷都是+2×10-6C,求它们所受的库仑力?