Question

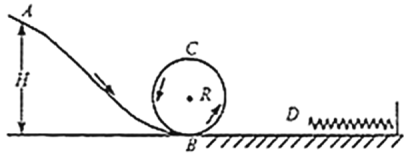
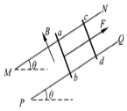
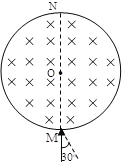
【题目】一半径为R的薄圆筒处于磁感应强度大小为B的匀强磁场中，磁场方向与筒的中心轴线平行，筒的横截面如图所示。图中直径MN的两端分别开有小孔，筒可绕其中心轴线转动，圆筒的转动方向和角速度大小可以通过控制装置改变。一不计重力的负电粒子从小孔M沿着MN方向射入磁场，当筒以大小为ω0的角速度转过90°时，该粒子恰好从某一小孔飞出圆筒。

（1）若粒子在筒内未与筒壁发生碰撞，求该粒子的荷质比和速率分别是多大？

（2）若粒子速率不变，入射方向在该截面内且与MN方向成30°角，则要让粒子与圆筒无碰撞地离开圆筒，圆筒角速度应为多大？

Answer 1

【答案】（1），，（2）或者其中n=0，1，2，3…。

【解析】

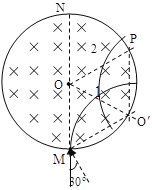
（1）若粒子沿MN方向入射，当筒转过90°时，粒子从M孔（筒逆时针转动）或N孔（筒顺时针转动）射出，如图，由轨迹1可知半径：

r=R

由：

粒子运动周期：

筒转过90°的时间：

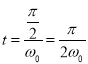
又：

联立以上各式得：荷质比，粒子速率；

（2）若粒子与MN方向成30°入射，速率不变半径仍为R，作粒子轨迹2如图，轨迹2圆心为，则四边形为菱形，可得：

所以，则粒子偏转的时间：

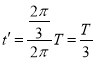
又：

得：，由于转动方向与射出孔不确定，讨论如下：

①当圆筒顺时针转动时，设筒转动的角速度变为ω1，若从N点离开，则筒转动时间满足：

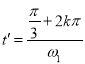
得：，其中k=0，1，2，3…

若从M点离开，则筒转动时间满足：

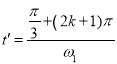
得：，其中k=0，1，2，3…；

综上可得：，其中n=0，1，2，3…；

②当圆筒逆时针转动时，设筒转动的角速度变为ω2，

若从M点离开，则筒转动时间满足：

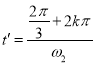
得：，其中k=0，1，2，3…；

若从N点离开，则筒转动时间满足：

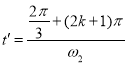
得：，其中k=0，1，2，3…；

综上可得，其中n=0,1,2,3…；

综上所述，圆筒角速度大小应为或者其中n=0，1，2，3…。