题目内容
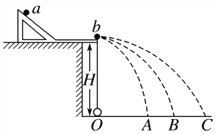
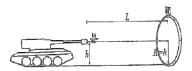
【题目】如图所示，装甲车在水平地面上以某一速度沿直线前进，车上机枪的枪管水平，距地面高为h=1.8m。在车正前方竖直立一块半径为1.8m的圆形靶，其底边与地面接触，枪口与靶距离为L时，机枪手正对把心射出第一发子弹，子弹的对地速度为
=824m/s.在子弹射出的同时，装甲车开始减速运动，行进s=92m后停下。装甲车停下后，机枪手以对地速度
=800m/s发射第二发子弹。(不计空气阻力，子弹看成质点，重力加速度g=10m/s)
(1)若L=412m，求第一发子弹留下的弹孔离靶心的距高。
(2)若L=412m，靶在第二发子弹射出的瞬间开始匀速转动。要使靶上的两个弹孔在同一条直线上，求靶转动角速度的可能值；
(3)若只有一发子弹能打中靶，求L的范围。
【答案】（1）
（2）
(n=1，2，3......) （3）494.4m<L≤572m.
【解析】试题分析：根据平抛公式即可求出第一发子弹留下的弹孔离靶心的距高；找出子弹飞行时间与把转动时间的关系即可解题；只有一发子弹能击中，若L太小，两发都能击中；若L太大，一发都击不中在结合运动学知识即可解题。
（1）子弹运动的时间为： 
，下落的高度为： 
（2）根据题意有： 
，
其中： 
(n=1，2，3......)
可得： 
(n=1，2，3......)
（3）只有一发子弹能击中，若L太小，两发都能击中；若L太大，一发都击不中
时间为： 
第一颗子弹打到靶的下沿时： 
第二颗子弹打到靶的下沿时： 
故L的范围为494.4m<L≤572m.
练习册系列答案
相关题目
