题目内容
【题目】如图所示,电动机带动滚轮做逆时针匀速转动,在滚轮的摩擦力作用下,将一金属板从斜面底端A送往上部,已知斜面光滑且足够长,倾角θ=30°,滚轮与金属板的切点B到斜面底端A距离L=6.5m,当金属板的下端运动到切点B处时,立即提起滚轮使它与板脱离接触.已知板的质量m=1kg,滚轮边缘线速度恒为v=4m/s,滚轮对板的正压力FN=20N,滚轮与金属板间的动摩擦因数为μ=0.35,取重力加速度g=10m/s2 . 求:
(1)板加速上升时所受到的滑动摩擦力大小;
(2)板加速至与滚轮边缘线速度相同时前进的距离;
(3)板匀速上升的时间.
【答案】
(1)解:根据摩擦力公式,得:f=μFN=0.35×20N=7N.
答:板加速上升时所受到的滑动摩擦力大小是70N;
(2)解:对板进行受力分析,根据牛顿第二定律:mgsinθ﹣f=ma
可以得到:a=2m/s2
根据运动学公式得:x= ![]() =
= ![]() m=4m
m=4m
答:板加速至与滚轮边缘线速度相同时前进的距离是4m;
(3)解:当板与轮的线速度相等后,板做匀速直线运动,则上升的时间为:
t= ![]() =
= ![]() s=0.625s
s=0.625s
答:板匀速上升的时间是0.625s.
【解析】本题重在对物体进行正确的受力分析,根据牛顿第二定律求解物体的加速度,联合运动学基本公式可以解决问题.
【考点精析】利用匀变速直线运动的速度、位移、时间的关系对题目进行判断即可得到答案,需要熟知速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值.

【题目】在“探究加速度与力、质量的关系"的实验中:
(1)某次实验中记录的纸带如图所示,从A点起每5个点取一个计数点,即两相邻计数点间的时间间隔为0.1s,则物体运动的加速度为__ m/s2(保留3位有效数字)
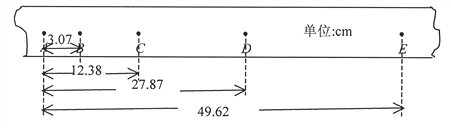 .
.
(2)在做“探究加速度与质量的关系"的实验时,若测得小车受力F一定时, a与m的关系数据如下表所示:
a/ (m·s-2) | 2.04 | 2.66 | 3.23 | 3.98 |
m/kg | 2.00 | 1.50 | 1.25 | 1.00 |
1/m/kg-1 | 0.50 | 0.67 | 0.80 | 1.00 |
①根据表中所列数据,分别在所给坐标系中作出a-m图象_____和a-1/m图象_____;
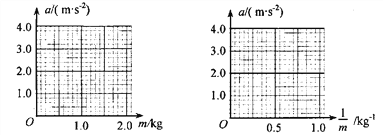
②对比分析a-m图象和a-1/m图象可知,当F一定时,a与m成___________比.

③由a-1/m图象可知,F=___________N(结果保留一位有效数字).



