题目内容
倾角30°的光滑斜面上,固定一质量为m=1kg的物块,物块到底端距离S=240米,物块受到一个平行于斜面向上的外力F作用,F的大小随时间周期性变化关系如图所示,t=ls时,由静止释放物块,求: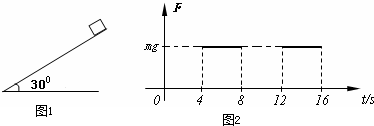
(1)4-8s内物体的加速度;
(2)物块下滑到斜面底端所用的时间;
(3)物块下滑到斜面底端过程中力F做的总功.

(1)4-8s内物体的加速度;
(2)物块下滑到斜面底端所用的时间;
(3)物块下滑到斜面底端过程中力F做的总功.
分析:(1)根据牛顿第二定律求出物体在4-8s内的加速度.
(2)根据牛顿第二定律知向下做匀加速直线运动的加速度和向上的加速度大小相等,物体在1~4s内向下匀加速直线运动,4~7s内向下匀减速至速度为0,7~8s内向上匀加速,8~9s向上匀减速至速度为0,完成一个周期,求出一个周期内的位移,从而确定几个周期到达底端.通过运动学公式求出)物块下滑到斜面底端所用的时间.
(3)求出物块到达底端的速度,根据动能定理求出物块下滑到斜面底端过程中力F做的总功.
(2)根据牛顿第二定律知向下做匀加速直线运动的加速度和向上的加速度大小相等,物体在1~4s内向下匀加速直线运动,4~7s内向下匀减速至速度为0,7~8s内向上匀加速,8~9s向上匀减速至速度为0,完成一个周期,求出一个周期内的位移,从而确定几个周期到达底端.通过运动学公式求出)物块下滑到斜面底端所用的时间.
(3)求出物块到达底端的速度,根据动能定理求出物块下滑到斜面底端过程中力F做的总功.
解答:解:(1)根据牛顿第二定律得,a2=
=5m/s2
方向平行于斜面向上
(2)1~4s内向下匀加速,a1=gsin30°=5m/s2,
s1=
a1t12=
m
4~7s内向下匀减速至速度为0,
a2=
=5m/s2.
s2=
a2t22=
m.
7~8s内向上匀加速,8~9s向上匀减速至速度为0,完成一个周期,
s3=s4=
a2×12=
m
一个周期内向下位移
△s=(s1+s2)-(s3+s4)=40m
S=240m=k△s,得k=6
由过程分析知,5个周期未能达到,第6个周期终点时刻之前,就已经到达.
下面我们计算第6个周期开始到达底端所用的时间t
第6个周期由总位移△s=40m,加速阶段t3=3s,
位移S1=
m,剩下位移,加力后它减速过程即可完成:
△s′=△s-s1=
m,
v0=5×3=15m/s,a=-5m/s2.
△s′=v0t4+
at42
代入数据得,
=15t4-
t42
得t4=3-
=1.6s.
t总=5T+t3+t4=40+3+1.6s=44.6s
(3)到达底端时速度v=v0+at4=15-5×1.6m/s=7m/s
根据动能定理得,WF+mgh=
mv2-0
解得WF=-11755J.
答:(1)4-8s内物体的加速度为5m/s2.
(2)物块下滑到斜面底端所用的时间为44.6s.
(3)物块下滑到斜面底端过程中力F做的总功为-11755J.
| F-mgsin30° |
| m |
方向平行于斜面向上
(2)1~4s内向下匀加速,a1=gsin30°=5m/s2,
s1=
| 1 |
| 2 |
| 45 |
| 2 |
4~7s内向下匀减速至速度为0,
a2=
| F-mgsin30° |
| m |
s2=
| 1 |
| 2 |
| 45 |
| 2 |
7~8s内向上匀加速,8~9s向上匀减速至速度为0,完成一个周期,
s3=s4=
| 1 |
| 2 |
| 5 |
| 2 |
一个周期内向下位移
△s=(s1+s2)-(s3+s4)=40m
S=240m=k△s,得k=6
由过程分析知,5个周期未能达到,第6个周期终点时刻之前,就已经到达.
下面我们计算第6个周期开始到达底端所用的时间t
第6个周期由总位移△s=40m,加速阶段t3=3s,
位移S1=
| 45 |
| 2 |
△s′=△s-s1=
| 35 |
| 2 |
v0=5×3=15m/s,a=-5m/s2.
△s′=v0t4+
| 1 |
| 2 |
代入数据得,
| 35 |
| 2 |
| 5 |
| 2 |
得t4=3-
| 2 |
t总=5T+t3+t4=40+3+1.6s=44.6s
(3)到达底端时速度v=v0+at4=15-5×1.6m/s=7m/s
根据动能定理得,WF+mgh=
| 1 |
| 2 |
解得WF=-11755J.
答:(1)4-8s内物体的加速度为5m/s2.
(2)物块下滑到斜面底端所用的时间为44.6s.
(3)物块下滑到斜面底端过程中力F做的总功为-11755J.
点评:解决本题的关键理清物体的运动规律,得出物体运动的周期性,结合牛顿第二定律、运动学公式、动能定理进行求解.

练习册系列答案
相关题目
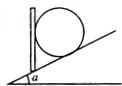 倾角α=30°的光滑斜面上放一重100N 的球,用光滑挡板把球挡住,如图所示.若不断改变挡板与斜面间的夹角,挡板对球的作用力大小也跟着改变,它可能出现的值有( )
倾角α=30°的光滑斜面上放一重100N 的球,用光滑挡板把球挡住,如图所示.若不断改变挡板与斜面间的夹角,挡板对球的作用力大小也跟着改变,它可能出现的值有( )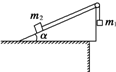 质量分别为m1和m2的两个小物块用轻绳连接,绳跨过位于倾角α=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,m1悬空,m2放在斜面上,用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间;第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上.如果
质量分别为m1和m2的两个小物块用轻绳连接,绳跨过位于倾角α=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,m1悬空,m2放在斜面上,用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间;第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上.如果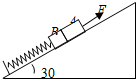 倾角30°的光滑斜面上并排放着质量分别是mA=10kg和mB=2kg的A、B两物块,劲度系数k=400N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,g取10m/s2,求F的最大值和最小值.
倾角30°的光滑斜面上并排放着质量分别是mA=10kg和mB=2kg的A、B两物块,劲度系数k=400N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,g取10m/s2,求F的最大值和最小值. (2010?新都区模拟)质量mA=10kg的物块A与质量mB=2kg的物块B放在倾角θ=30°的光滑斜面上处于静止状态,轻质弹簧一端与物块B连接,另一端与固定档板连接,弹簧的劲度系数k=400N/m,现给物块A施加一个平行于斜面向上的F,使物块A沿斜面向上做匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,求:(g=10m/s2)
(2010?新都区模拟)质量mA=10kg的物块A与质量mB=2kg的物块B放在倾角θ=30°的光滑斜面上处于静止状态,轻质弹簧一端与物块B连接,另一端与固定档板连接,弹簧的劲度系数k=400N/m,现给物块A施加一个平行于斜面向上的F,使物块A沿斜面向上做匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,求:(g=10m/s2)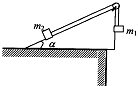 (2005?盐城三模)质量分别为m1和m2的两个小物块用轻绳连结,绳跨过位于长为L倾角α=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,m1悬空,m2放在斜面上,m2自斜面底端由静止开始运动至斜面顶端时速度为V.第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上,发现m1自斜面底端由静止开始运动至斜面顶端时速度为V/3.求m1和m2之比.
(2005?盐城三模)质量分别为m1和m2的两个小物块用轻绳连结,绳跨过位于长为L倾角α=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,m1悬空,m2放在斜面上,m2自斜面底端由静止开始运动至斜面顶端时速度为V.第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上,发现m1自斜面底端由静止开始运动至斜面顶端时速度为V/3.求m1和m2之比.