题目内容
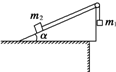 质量分别为m1和m2的两个小物块用轻绳连接,绳跨过位于倾角α=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,m1悬空,m2放在斜面上,用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间;第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上.如果
质量分别为m1和m2的两个小物块用轻绳连接,绳跨过位于倾角α=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,m1悬空,m2放在斜面上,用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间;第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上.如果| m1 |
| m2 |
| 11 |
| 19 |
分析:根据牛顿第二定律分别求出两次两物体的加速度大小,由位移公式求出时间之比,再求出第二次时m1自斜面底端由静止开始运动至斜面顶端所需的时间.
解答:解:根据牛顿第二定律得:
第一次:a1=
①
第二次:a2=
②
由②:①得,a2:a1=9:1
由位移公式x=
at2得,t1:t2=
:
=1:3
又t1=t,得到,t2=
t
答:第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上,m1自斜面底端由静止开始运动至斜面顶端所需的时间为
t.
第一次:a1=
| m1g-m2gsin30° |
| m1+m2 |
第二次:a2=
| m2g-m1gsin30° |
| m1+m2 |
由②:①得,a2:a1=9:1
由位移公式x=
| 1 |
| 2 |
| a1 |
| a2 |
又t1=t,得到,t2=
| 1 |
| 3 |
答:第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上,m1自斜面底端由静止开始运动至斜面顶端所需的时间为
| 1 |
| 3 |
点评:本题是牛顿第二定律与运动学结合处理动力学问题,采用整体法求加速度,也可以运用隔离法求加速度.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
两颗行星的质量分别为m1和m2,绕太阳运行的轨道半长轴分别为r1和r2,则它们的公转周期之比为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、无法确定 |
 一对双星,是由相距L、质量分别为M1和M2的两颗星体构成,两星间引力很大但又未吸引到一起,是因为它们以连线上某点为圆心做圆周运动的结果,如图所示,试求它们各自运转半径和角速度各是多少?
一对双星,是由相距L、质量分别为M1和M2的两颗星体构成,两星间引力很大但又未吸引到一起,是因为它们以连线上某点为圆心做圆周运动的结果,如图所示,试求它们各自运转半径和角速度各是多少? 如图所示,水平放置的金属平行板的B板接地,A板电势为+U,两板间距离为d.d比两板间的尺寸小很多,在两板之间有一长为l的绝缘轻杆,可绕固定轴O在竖直面内无摩擦地自由转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,m1<m2,它们的带电量分别为-q1和+q2,q1<q2,当杆由图示水平位置从静止开始转到竖直位置时( )
如图所示,水平放置的金属平行板的B板接地,A板电势为+U,两板间距离为d.d比两板间的尺寸小很多,在两板之间有一长为l的绝缘轻杆,可绕固定轴O在竖直面内无摩擦地自由转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,m1<m2,它们的带电量分别为-q1和+q2,q1<q2,当杆由图示水平位置从静止开始转到竖直位置时( )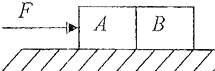 如图所示,质量分别为m1和m2的A、B两物体放置在粗糙水平桌面上,恒力F作用在A物体上,则以下说法正确的是( )
如图所示,质量分别为m1和m2的A、B两物体放置在粗糙水平桌面上,恒力F作用在A物体上,则以下说法正确的是( )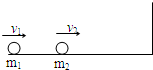 (1)(3-5)在汤姆孙发现电子后,对于原子中正负电荷的分布的问题,科学家们提出了许多模型,最后他们认定:占原子质量绝大部分的正电荷集中在很小的空间范围内,电子绕正电荷旋转.此模型称原子的有核模型.最先提出原子有核模型的科学家是
(1)(3-5)在汤姆孙发现电子后,对于原子中正负电荷的分布的问题,科学家们提出了许多模型,最后他们认定:占原子质量绝大部分的正电荷集中在很小的空间范围内,电子绕正电荷旋转.此模型称原子的有核模型.最先提出原子有核模型的科学家是