题目内容
 (2010?新都区模拟)质量mA=10kg的物块A与质量mB=2kg的物块B放在倾角θ=30°的光滑斜面上处于静止状态,轻质弹簧一端与物块B连接,另一端与固定档板连接,弹簧的劲度系数k=400N/m,现给物块A施加一个平行于斜面向上的F,使物块A沿斜面向上做匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,求:(g=10m/s2)
(2010?新都区模拟)质量mA=10kg的物块A与质量mB=2kg的物块B放在倾角θ=30°的光滑斜面上处于静止状态,轻质弹簧一端与物块B连接,另一端与固定档板连接,弹簧的劲度系数k=400N/m,现给物块A施加一个平行于斜面向上的F,使物块A沿斜面向上做匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,求:(g=10m/s2)(1)力F的最大值与最小值
(2)力F由最小值到最大值的过程中,物块A所增加的重力势能.
分析:(1)先根据平衡条件求出弹簧开始的压缩量,因为在前0.2 s时间内,F为变力,0.2s以后,F为恒力,所以在0.2s时,A、B分离,B对A的作用力为0,对物体B运用牛顿第二定律列式得出F与加速度的关系式,当A、B开始运动时拉力最小,当A、B分离时拉力最大,根据牛顿第二定律即可求解;
(2)求解出加速度后,根据位移时间关系公式列式求出物块A所增加的高度,即可求出物块A所增加的重力势能.
(2)求解出加速度后,根据位移时间关系公式列式求出物块A所增加的高度,即可求出物块A所增加的重力势能.
解答:解:(1)设刚开始时弹簧压缩量为x0,则(mA+mB)gsin θ=kx0…①
因为在前0.2 s时间内,F为变力,0.2 s以后,F为恒力,所以在0.2 s时,B对A的作用力为0,
由牛顿第二定律知:kx1-mBgsin θ=mBa…②
前0.2 s时间内A、B向上运动的距离为:x0-x1=
at2…③
①②③式联立解得:a=5 m/s2
当A、B开始运动时拉力最小,此时有:Fmin=(mA+mB)a=60N
当A、B分离时拉力最大,此时有:Fmax=mA(a+gsin θ)=100N.
(2)物体上升的位移为:x=
at2=
×5×0.04=0.1m
故上升的高度为:h=x?sin30°=
x=0.05m
物块A所增加的重力势能为△EP=mAgh=5J.
答:
(1)力F的最大值与最小值分别为100N和60N.
(2)力F由最小值到最大值的过程中,物块A所增加的重力势能为5J.
因为在前0.2 s时间内,F为变力,0.2 s以后,F为恒力,所以在0.2 s时,B对A的作用力为0,
由牛顿第二定律知:kx1-mBgsin θ=mBa…②
前0.2 s时间内A、B向上运动的距离为:x0-x1=
| 1 |
| 2 |
①②③式联立解得:a=5 m/s2
当A、B开始运动时拉力最小,此时有:Fmin=(mA+mB)a=60N
当A、B分离时拉力最大,此时有:Fmax=mA(a+gsin θ)=100N.
(2)物体上升的位移为:x=
| 1 |
| 2 |
| 1 |
| 2 |
故上升的高度为:h=x?sin30°=
| 1 |
| 2 |
物块A所增加的重力势能为△EP=mAgh=5J.
答:
(1)力F的最大值与最小值分别为100N和60N.
(2)力F由最小值到最大值的过程中,物块A所增加的重力势能为5J.
点评:从受力角度看,两物体分离的条件是两物体间的正压力为0.从运动学角度看,一起运动的两物体恰好分离时,两物体在沿斜面方向上的加速度和速度仍相等.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目

 (2010?新都区模拟)如图所示,用长为L的轻绳把一个小铁球悬挂在高2L的O点处,小铁球以O为圆心在竖直平面内做圆周运动且恰能到达最高点B处,若运动中轻绳断开,则小铁球落到地面时的速度大小为( )
(2010?新都区模拟)如图所示,用长为L的轻绳把一个小铁球悬挂在高2L的O点处,小铁球以O为圆心在竖直平面内做圆周运动且恰能到达最高点B处,若运动中轻绳断开,则小铁球落到地面时的速度大小为( ) (2010?新都区模拟)(1)为了响应国家的“节能减排”号召,某同学采用了一个家用汽车的节能方法.在符合安全行驶的要求的情况下,通过减少汽车后备箱中放置的不常用物品和控制加油量等措施,使汽车负载减少.假设汽车以72km/h的速度行驶时,负载改变前、后汽车受到阻力分别为2000N和1950N.请计算该方法使发动机输出功率减少了多少?
(2010?新都区模拟)(1)为了响应国家的“节能减排”号召,某同学采用了一个家用汽车的节能方法.在符合安全行驶的要求的情况下,通过减少汽车后备箱中放置的不常用物品和控制加油量等措施,使汽车负载减少.假设汽车以72km/h的速度行驶时,负载改变前、后汽车受到阻力分别为2000N和1950N.请计算该方法使发动机输出功率减少了多少?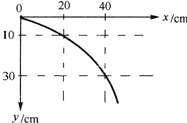 (2010?新都区模拟)在“研究平抛物体的运动”实验中
(2010?新都区模拟)在“研究平抛物体的运动”实验中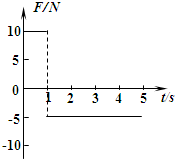 (2010?新都区模拟)如图所示,图线表示作用在某物体上的合外力跟时间变化的关系,若物体开始时是静止的,那么( )
(2010?新都区模拟)如图所示,图线表示作用在某物体上的合外力跟时间变化的关系,若物体开始时是静止的,那么( )