��Ŀ����
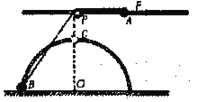
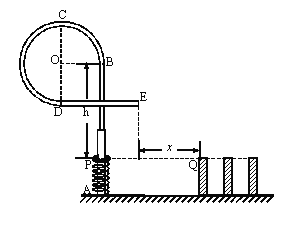
����Ŀ���������пƼ�������Ŀ��ͬѧ��һ������������Ϸ�У������һ����ͼ��ʾ����ʼ����װ�ã�AB���dz��������ɵ�����ֱ�����ˣ�BCD���ǰ뾶ΪR���ķ�֮��Բ����ˣ�DE���dz���Ϊ2R��ˮƽ�ˣ���AB�����Դ�������ֱ���������¶˹̶��Ҿ���ϵ���ϴ�����ʵ��ɣ��ڵ����϶˷�������Ϊm������ÿ�ν����ɵij���ѹ����P�����������PB�ĸ߶Ȳ�Ϊh����������ɿɽ����������ڴ��������Ҳ��ж���ŵ���ƣ�����ŵ���Ƶ������ߵ�Q��P��ȸߣ�����E��ˮƽ����Ϊx(���Ե���)����֪��������ʱ�ĵ�������Ep=10mgR����P��ˮƽ��DE�εĶ�Ħ��������=0.5�����������ֵ�Ħ�����Ժ��Բ��ƣ��������ܵ��Ŀ����������������ʱ�ĵ���������ʧ��������������ֱ�˴�ϸ�仯������Ӱ�죬�������ٶ�Ϊg����
(1)��h=7Rʱ��������˵���ߵ�C��ʱ���ٶȴ�С��
(2)��(1)�������˶�����ߵ�Cʱ�Ը��������Ĵ�С�ͷ���
(3)��h��3R��10R�����ɵ���Ҫʹ����ǡ�ܻ���Q�㣬��xӦ�����ĸ���Χ�ڵ��ڣ�
���𰸡���1��![]() ����2��3mg����ֱ���ϣ���3��
����2��3mg����ֱ���ϣ���3��![]() ��x��9R
��x��9R
�������������������1����h=3Rʱ������P���˶���C�㣬���ݻ�е���غ㶨�����v��
��2������ߵ�Cʱ������������ţ�ٵڶ����������������
��3����ǡ�ܻ���Q�㣬��ƽ���˶����̷ֽ�Ϊˮƽ�������ֱ������˶����ٴ�P��E�����������غ㶨�����߶�h��
�⣺(1)��h=7Rʱ������P���˶���C�㣬���ݻ�е���غ㶨���У� ![]()
![]() ����ã�
����ã� ![]() ��
��
(2) ����ߵ�Cʱ������������ţ�ٵڶ������У�
![]()
��ã� ![]() ���������ϣ�
���������ϣ�
(3) ��ǡ�ܻ���Q�㣬ƽ���˶����̣�
![]()
![]()
��P��E�����������غ㶨���У� ![]()
�����ϸ�ʽ�ɽ�ã� ![]() ��
��
���磺���⿼����Բ���˶���ߵ�Ķ���ѧ�����Լ���е���غ㶨�ɵ�Ӧ�ã�֪��Բ���˶�����������Դ���Լ�ƽ���˶���ˮƽ�������ֱ�����ϵ��˶������ǽ������Ĺؼ���