题目内容
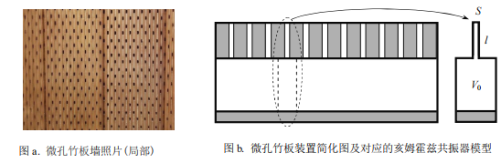
【题目】2016年9月,G20峰会在杭州隆重召开,其会议厅的装饰设计既展示出中国建筑的节能环保理念,又体现了浙江的竹文化特色。图a给出了其部分墙面采用的微孔竹板装饰的局部放大照片,该装饰同时又实现了对声波的共振吸收.竹板上有一系列不同面积、周期性排列的长方形微孔,声波进入微孔后导致微孔中的空气柱做简谐振动.单个微孔和竹板后的空气层,可简化成一个亥姆霍兹共振器,如图b所示.假设微孔深度均为l、单个微孔后的空气腔体体积均为![]() 、微孔横截面积记为S.声波在空气层中传播可视为绝热过程,声波传播速度
、微孔横截面积记为S.声波在空气层中传播可视为绝热过程,声波传播速度![]() 与空气密度
与空气密度![]() 及体积弹性模量
及体积弹性模量![]() 的关系为
的关系为![]() ,其中
,其中![]() 是气体压强的增加量
是气体压强的增加量![]() 与其体积V相对变化量之比
与其体积V相对变化量之比![]() ,已知标准状态(273K,latm=1.01×105Pa)下空气(可视为理想气体)的摩尔质量Mmol=29.0g/mol,热容比
,已知标准状态(273K,latm=1.01×105Pa)下空气(可视为理想气体)的摩尔质量Mmol=29.0g/mol,热容比![]() ,气体普适常量R=8.31J/(K·mol).
,气体普适常量R=8.31J/(K·mol).
(1)求标准状态下空气的密度和声波在空气中的传播速度![]() ;
;
(2)求上述亥姆霍兹共振器吸收声波的频率(用![]() 、S、I、V0表示);
、S、I、V0表示);
(3)为了吸收频率分别为120Hz和200Hz的声波,相应的两种微孔横截面积之比应为多少?
【答案】(1)![]() (2)
(2)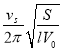 (3)
(3)![]()
【解析】
(1)由理想气体状态方程有
![]() (1)
(1)
式中,P、V和T分别为空气的压强、体积和(绝对)温度,M和Mmol分别为空气总质量和;摩尔质量。由(1)式得空气密度为
![]()
在标准状态下(以下标“标”表示)有,
![]() (2)
(2)
理想气体的绝热过程满足
![]() =常量
=常量
式中γ是热容比。对上式两边微分得
![]() (3)
(3)
由(3)式可得,空气的体积弹性模量为
![]() (4)
(4)
声波在空气中的传播速度为
![]()
在标准状态下有
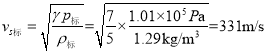 (5)
(5)
(2)细管内的空气柱的质量为
![]() (6)
(6)
细管中的空气柱的运动是由外界压力与容器内的压力之差所引起的.设这部分空气柱运动的位移为x(向外为正),容器内的空气体积的改变为
![]() (7)
(7)
容器内气体压力的变化满足绝热过程,由(3)式有
![]() (8)
(8)
相应地,对于细管内运动着的空气柱的作用力为
![]() (9)
(9)
从而,细管内空气柱的运动方程可写为
![]() (10)
(10)
(10)式可写成
![]() (11)
(11)
这是简谐振动的方程,o是简谐振动的圆频率
![]() (12)
(12)
将![]() 代入(10)式得,所述亥姆霍兹共振器吸收声波的频率为
代入(10)式得,所述亥姆霍兹共振器吸收声波的频率为
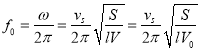 (13)
(13)
上式最后一步利用了单个微孔后的空气腔体体积为![]() .
.
(3)按题设,两种需要通过所述亥姆霍兹共振器吸收声波的频率![]() 和
和![]() 之比为
之比为
![]() (14)
(14)
由(13)式可得
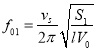 ,
, (15)
(15)
式中,S1和S2是相应的上述亥姆霍兹共振器的微孔的横截面积.由(15)式有
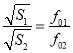 (16)
(16)
即
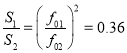 (17)
(17)

 口算能手系列答案
口算能手系列答案