题目内容
【题目】真空中的某装置如图所示,其中平行金属板A,B之间有加速电场,C,D之间有偏转电场,M为荧光屏,今有质子,氘核和α粒子均由A板从静止开始被加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )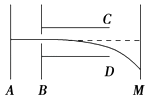
A.三种粒子从B板运动到荧光屏经历的时间不同
B.三种粒子打到荧光屏上的位置相同
C.偏转电场的电场力对三种粒子做功之比为1:2:2
D.偏转电场的电场力对三种粒子做功之比为1:2:4
【答案】A,B
【解析】解:设AB间的电压为U1 , CD间的电压为U2、板长为L、板距为d,CD右边缘离荧光屏的距离为S,从一般情况考虑,在加速电场中有: ![]() ①,进入偏转电场做类平抛运动.
①,进入偏转电场做类平抛运动.
A、穿出CD后的时间  ,由于三种粒子的比荷
,由于三种粒子的比荷 ![]() 不同,所以三种粒子穿出CD板的时间不同,所以选项A正确.
不同,所以三种粒子穿出CD板的时间不同,所以选项A正确.
B、偏移的距离: ![]() ,偏转角的正切:
,偏转角的正切: 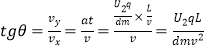 以上两式 联立①式得:
以上两式 联立①式得: ![]() ,
, ![]() ,由两式可以看出,三种粒子从CD边缘的同一点穿出,且速度方向相同,那么最后打到荧光屏的位置相同,所以选项B正确.
,由两式可以看出,三种粒子从CD边缘的同一点穿出,且速度方向相同,那么最后打到荧光屏的位置相同,所以选项B正确.
CD、偏转电场对三种粒子所做功 ![]() ,则做功之比等于电量之比为1:1:2,所以选项CD错误.
,则做功之比等于电量之比为1:1:2,所以选项CD错误.
故选:AB
【考点精析】利用带电微粒(计重力)在电场中的运动对题目进行判断即可得到答案,需要熟知带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或明确的暗示以外,一般都不能忽略重力;由于带电粒子在匀强电场中所受电场力与重力都是恒力,因此可以用两种方法处理:①正交分解法;②等效“重力”法.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】某同学探究弹力与弹簧伸长量的关系.
①将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧时,长度记为L0 , 弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6 , 数据如下表表:
代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 35.35 | 37.40 | 39.30 |
表中有一个数值记录不规范,代表符号为 . 由表可知所用刻度尺的最小长度为 .
③图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与的差值(填“L0或L1”).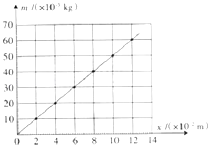
④由图可知弹簧的劲度系数为N/m;通过图和表可知砝码盘的质量为g(结果保留两位有效数字,重力加速度取9.8m/s2).