题目内容
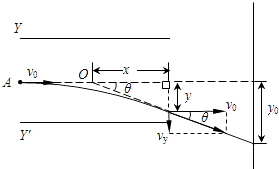
【题目】如图所示,真空中水平放置的两个相同极板Y和Y'长为L,相距d,足够大的竖直屏与两板右侧相距b.在两板间加上可调偏转电压U,一束质量为m、带电量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出.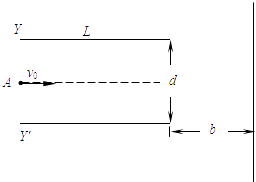
(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点;
(2)求两板间所加偏转电压U的范围;
(3)求粒子可能到达屏上区域的长度.
【答案】
(1)
解:设粒子在运动过程中的加速度大小为a,离开偏转电场时偏转距离为y,沿电场方向的速度为vy,偏转角为θ,其反向延长线通过O点,O点与板右端的水平距离为x,则有
侧移量,y= ![]() ①
①
匀速运动的位移,L=v0t②
竖直方向的速度,vy=at
![]()
联立可得 ![]()
即粒子飞出电场后的速度方向的反向延长线交于两板间的中心.
(2)
解:由牛顿第二定律,则有 ![]() ③
③
电场强度与电势差的关系,E= ![]() ④
④
由①②③④式解得 ![]()
当 ![]() 时,
时, ![]()
则两板间所加电压的范围 ![]()
(3)
解:当 ![]() 时,粒子在屏上侧向偏移的距离最大(设为y0),则
时,粒子在屏上侧向偏移的距离最大(设为y0),则
![]()
而tan ![]()
解得 ![]()
则粒子可能到达屏上区域的长度为 ![]()
【解析】(1)画出运动轨迹图,根据运动学公式与牛顿第二定律,及三角函数关系,从而即可证明;(2)由牛顿第二定律与公式E= ![]() 相结合,可求得结果;(3)运用几何关系,结合偏角与位移的关系,从而即可求解.
相结合,可求得结果;(3)运用几何关系,结合偏角与位移的关系,从而即可求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目