题目内容
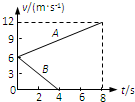 两个完全相同的物块A、B质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示受到水平拉力F作用的A物块和不受拉力作用的B物块的v-t图线.取g=10m/s2.求:
两个完全相同的物块A、B质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示受到水平拉力F作用的A物块和不受拉力作用的B物块的v-t图线.取g=10m/s2.求:(1)物块与水平面间的动摩擦因数μ;
(2)物块A所受拉力F的大小;
(3)B刚好停止运动时刻物块A、B之间的距离d.
分析:(1)根据v-t图象的斜率等于加速度,求出B物块的加速度,由牛顿第二定律求出动摩擦因数;
(2)由v-t图象求出,A的加速度,由牛顿第二定律列方程,求出物体A所受拉力F的大小;
(3)4s末B物体静止,由图象的“面积”求出A、B之间的距离s.
(2)由v-t图象求出,A的加速度,由牛顿第二定律列方程,求出物体A所受拉力F的大小;
(3)4s末B物体静止,由图象的“面积”求出A、B之间的距离s.
解答:解:(1)根据v-t图象的斜率等于加速度,则得:
B物块的加速度大小为:aB=
=
m/s2=1.5m/s2
由牛顿第二定律得:μmg=maB,解得:μ=
=
=0.15;
(2)由图象得:
A物块的加速度大小为:aA=
=
m/s2=0.5m/s2;
由牛顿第二定律得:F-f=ma1,
解得:F=1.8N;
(3)4s末B物体刚好停止运动,设A、B在4s内的位移分别为S1、S2,
由v-t图得:S1=
×(6+9)×4m=30m,
S2=
×6×4m=12m,
12s末A、B两物体间的距离S=S1-S2=30m-12m=18m.
答:
(1)物块与水平面间的动摩擦因数μ为0.15;
(2)物块A所受拉力F的大小为1.8N;
(3)B刚好停止运动时刻物块A、B之间的距离d为18m.
B物块的加速度大小为:aB=
| △vB |
| △tB |
| 6 |
| 4 |
由牛顿第二定律得:μmg=maB,解得:μ=
| aB |
| g |
| 1.5 |
| 10 |
(2)由图象得:
A物块的加速度大小为:aA=
| △vA |
| △tA |
| 12-6 |
| 8 |
由牛顿第二定律得:F-f=ma1,
解得:F=1.8N;
(3)4s末B物体刚好停止运动,设A、B在4s内的位移分别为S1、S2,
由v-t图得:S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
12s末A、B两物体间的距离S=S1-S2=30m-12m=18m.
答:
(1)物块与水平面间的动摩擦因数μ为0.15;
(2)物块A所受拉力F的大小为1.8N;
(3)B刚好停止运动时刻物块A、B之间的距离d为18m.
点评:本题首先要根据斜率求出加速度、“面积”求出位移,其次抓住两物体的滑动摩擦力相同.

练习册系列答案
相关题目
 (2012?葫芦岛模拟)两个完全相同的物块A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象,求:
(2012?葫芦岛模拟)两个完全相同的物块A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象,求: 两个完全相同的物块a、b,在水平面上以相同的初速度从同一位置开始运动,图中a直线表示a物体不受拉力作用、b直线表示b物体受到水平拉力F=1.8N作用的υ-t图象,求:
两个完全相同的物块a、b,在水平面上以相同的初速度从同一位置开始运动,图中a直线表示a物体不受拉力作用、b直线表示b物体受到水平拉力F=1.8N作用的υ-t图象,求: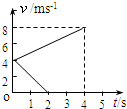 两个完全相同的物块A、B,质量均为m=0.8kg,沿同一粗糙水平面以相同的初速度从同一位置运动,它们速度随时间的变化关系如图所示,图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象.求:
两个完全相同的物块A、B,质量均为m=0.8kg,沿同一粗糙水平面以相同的初速度从同一位置运动,它们速度随时间的变化关系如图所示,图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象.求: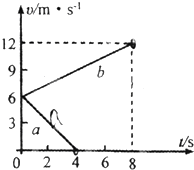 两个完全相同的物块a、b质量为m=0.8kg,在水平面上以相同的初速度从同一位置开始运动,图中的两条直线表示物体受到水平拉力F作用和不受拉力作用的υ-t图象,求:
两个完全相同的物块a、b质量为m=0.8kg,在水平面上以相同的初速度从同一位置开始运动,图中的两条直线表示物体受到水平拉力F作用和不受拉力作用的υ-t图象,求: