题目内容
 (2012?葫芦岛模拟)两个完全相同的物块A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象,求:
(2012?葫芦岛模拟)两个完全相同的物块A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象,求:(1)物块A所受拉力F的大小;
(2)8s末物块A、B之间的距离x.
分析:(1)由速度时间图象得到物体的运动规律,然后根据速度时间公式求出加速度,再对物体受力分析,根据牛顿第二定律列方程求解即可;
(2)根据平均速度公式分别求出物体AB的位移,得到两个物体的间距.
(2)根据平均速度公式分别求出物体AB的位移,得到两个物体的间距.
解答:解:(1)设A、B两物块的加速度分别为a1、a2,由v-t图象可知:A的初速度v0=6m/s,A物体的末速度v1=12m/s,B物体的速度v2=0,根据速度时间公式,有
a1=
=0.75m/s2 ①
a2=
=1.5m/s2 ②
对A、两物块分别由牛顿第二定律得:
F-Ff=ma1 ③
Ff=ma2 ④
由①②③④可得:F=1.8N
即物块A所受拉力F的大小为1.8N.
(2)设A、B两物块8s内的位移分别为x1、x2由图象得:
x1=
t1=72m
x2=
t2=12m
所以x=x1-x2=60 m
即8s末物块A、B之间的距离x为60m.
a1=
| △v1 |
| △t1 |
a2=
| △v2 |
| △t2 |
对A、两物块分别由牛顿第二定律得:
F-Ff=ma1 ③
Ff=ma2 ④
由①②③④可得:F=1.8N
即物块A所受拉力F的大小为1.8N.
(2)设A、B两物块8s内的位移分别为x1、x2由图象得:
x1=
| v0+v1 |
| 2 |
x2=
| v0+v2 |
| 2 |
所以x=x1-x2=60 m
即8s末物块A、B之间的距离x为60m.
点评:本题关键是根据速度时间图象得到两物体的运动情况,然后根据运动学公式、牛顿第二定律列方程并联立方程组求解.

练习册系列答案
相关题目
 (2012?葫芦岛模拟)如图所示,一个质量为m=2.0×10-11kg,电荷量q=+1.0×10-5C的带电微粒(重力忽略不计),从静止开始经U1=100V电场加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压U2=50V.金属板长L=20cm,两板间距d=
(2012?葫芦岛模拟)如图所示,一个质量为m=2.0×10-11kg,电荷量q=+1.0×10-5C的带电微粒(重力忽略不计),从静止开始经U1=100V电场加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压U2=50V.金属板长L=20cm,两板间距d= (2012?葫芦岛模拟)如图所示,光滑水平面上放置质量分别为m、2m和3m的三个木块,其中质量为2m和3m的木块间用一不可伸长的轻绳相连,轻绳能承受的最大拉力为T.现用水平拉力F拉其中一个质量为3m的木块,使三个木块以同一加速度运动,则以下说法正确的是( )
(2012?葫芦岛模拟)如图所示,光滑水平面上放置质量分别为m、2m和3m的三个木块,其中质量为2m和3m的木块间用一不可伸长的轻绳相连,轻绳能承受的最大拉力为T.现用水平拉力F拉其中一个质量为3m的木块,使三个木块以同一加速度运动,则以下说法正确的是( ) (2012?葫芦岛模拟)某一阻值不变的纯电阻元件(阻值R在50Ω~100Ω之间),额定功率为0.25W.要用伏安法较准确地测量它的阻值,实验器材有:
(2012?葫芦岛模拟)某一阻值不变的纯电阻元件(阻值R在50Ω~100Ω之间),额定功率为0.25W.要用伏安法较准确地测量它的阻值,实验器材有: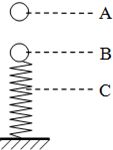 (2012?葫芦岛模拟)如图所示,一小球自A点由静止自由下落到B点时与弹簧接触.到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
(2012?葫芦岛模拟)如图所示,一小球自A点由静止自由下落到B点时与弹簧接触.到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )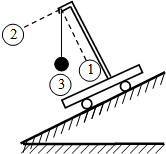 (2012?葫芦岛模拟)一个单摆悬挂在小车上,随小车沿着斜面滑下,图中的虚线①与斜面垂直,虚线②沿斜面方向,则可判断出( )
(2012?葫芦岛模拟)一个单摆悬挂在小车上,随小车沿着斜面滑下,图中的虚线①与斜面垂直,虚线②沿斜面方向,则可判断出( )