题目内容
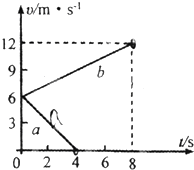 两个完全相同的物块a、b质量为m=0.8kg,在水平面上以相同的初速度从同一位置开始运动,图中的两条直线表示物体受到水平拉力F作用和不受拉力作用的υ-t图象,求:
两个完全相同的物块a、b质量为m=0.8kg,在水平面上以相同的初速度从同一位置开始运动,图中的两条直线表示物体受到水平拉力F作用和不受拉力作用的υ-t图象,求:(1)物块b所受拉力F的大小;
(2)8s末a、b间的距离;
(3)若在8s末将作用在b物体上的水平拉力F换到a物体上,在a追上b之前再过多长时间它们相距最远?最远距离为多少?
分析:ab两物体完全相同,且在同一水平面上运动,由图象可得两物体的加速度,根据牛顿第二定律可求得物体a所受摩擦力,从而根据牛顿第二定律可求得b所受拉力;
由位移时间公式可求得ab两物体的位移;
8s末将作用在b物体上的水平拉力F换到a物体上,a做初速度为0的加速度aa=
m/s2的匀加速运动,b做初速度为12m/s,
加速度为ab=-
m/s2的匀减速直线运动,当二者速度相等时,两物体相距最远.由速度公式求出时间,由位移公式求出两车间的距离.
由位移时间公式可求得ab两物体的位移;
8s末将作用在b物体上的水平拉力F换到a物体上,a做初速度为0的加速度aa=
| 3 |
| 4 |
加速度为ab=-
| 3 |
| 2 |
解答:解:(1)由图象可得,物体a、b的加速度分别为:
aa=
=-
m/s2
ab=
=
m/s2
故物体所受摩擦力f=maa=0.8×
=1.2N
对b由F-f=mab
可得:物块b所受拉力F=f+mab=1.2+0.8×
=1.8N
(2)8s内,物体b的位移xb=v0t+
abt2=6×8+
×
×82=72m
对物体a右图可这在t=4s时已静止,所以物体a在8s内的位移实际是在4s内的位移
即:xa=
×6×4=12m
故8s末a、b间的距离△x=xb-xa=72-12=60m
(3)在8s末将作用在b物体上的水平拉力F换到a物体上,则
a做初速度为0的加速度aa=
m/s2的匀加速运动,b做初速度为12m/s,
加速度为ab=-
m/s2的匀减速直线运动,当二者速度相等时,两物体相距最远.
vb-abt=va
即:12-
t=
t
解得:t=
s
b的位移:sb=vbt-
abt2=12×
-
×
×(
)2=64-
a的位移:sa=
aat2=
×
×(
)2=
故△X=sb-sa+△x=64-
-
+60=92m
答:(1)物块b所受拉力F的大小为1.8N;(2)8s末a、b间的距离为60m;(3)在a追上b之前再过
s它们相距最远,最远距离为92m
aa=
| 0-6 |
| 4 |
| 3 |
| 2 |
ab=
| 12-6 |
| 8 |
| 3 |
| 4 |
故物体所受摩擦力f=maa=0.8×
| 3 |
| 2 |
对b由F-f=mab
可得:物块b所受拉力F=f+mab=1.2+0.8×
| 3 |
| 4 |
(2)8s内,物体b的位移xb=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
对物体a右图可这在t=4s时已静止,所以物体a在8s内的位移实际是在4s内的位移
即:xa=
| 1 |
| 2 |
故8s末a、b间的距离△x=xb-xa=72-12=60m
(3)在8s末将作用在b物体上的水平拉力F换到a物体上,则
a做初速度为0的加速度aa=
| 3 |
| 4 |
加速度为ab=-
| 3 |
| 2 |
vb-abt=va
即:12-
| 3 |
| 2 |
| 3 |
| 4 |
解得:t=
| 16 |
| 3 |
b的位移:sb=vbt-
| 1 |
| 2 |
| 16 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 16 |
| 3 |
| 64 |
| 3 |
a的位移:sa=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 16 |
| 3 |
| 32 |
| 3 |
故△X=sb-sa+△x=64-
| 64 |
| 3 |
| 32 |
| 3 |
答:(1)物块b所受拉力F的大小为1.8N;(2)8s末a、b间的距离为60m;(3)在a追上b之前再过
| 16 |
| 3 |
点评:本题考查牛顿第二定律和运动学公式,第(3)在分别研究两物体运动情况的基础上,关键要抓住两物体之间的关系,比如速度关系、位移关系.

练习册系列答案
相关题目
 (2012?葫芦岛模拟)两个完全相同的物块A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象,求:
(2012?葫芦岛模拟)两个完全相同的物块A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象,求: 两个完全相同的物块a、b,在水平面上以相同的初速度从同一位置开始运动,图中a直线表示a物体不受拉力作用、b直线表示b物体受到水平拉力F=1.8N作用的υ-t图象,求:
两个完全相同的物块a、b,在水平面上以相同的初速度从同一位置开始运动,图中a直线表示a物体不受拉力作用、b直线表示b物体受到水平拉力F=1.8N作用的υ-t图象,求: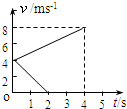 两个完全相同的物块A、B,质量均为m=0.8kg,沿同一粗糙水平面以相同的初速度从同一位置运动,它们速度随时间的变化关系如图所示,图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象.求:
两个完全相同的物块A、B,质量均为m=0.8kg,沿同一粗糙水平面以相同的初速度从同一位置运动,它们速度随时间的变化关系如图所示,图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象.求: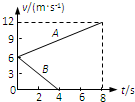 两个完全相同的物块A、B质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示受到水平拉力F作用的A物块和不受拉力作用的B物块的v-t图线.取g=10m/s2.求:
两个完全相同的物块A、B质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示受到水平拉力F作用的A物块和不受拉力作用的B物块的v-t图线.取g=10m/s2.求: