Question

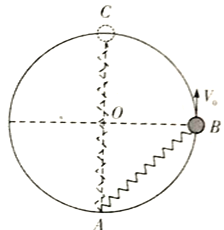
【题目】如图所示，有界的匀强磁场磁感应强度为B=0.05T，磁场方向垂直于纸面向里，MN是磁场的左边界．在磁场中A处放一个放射源，内装 Ra， Ra放出某种射线后衰变成 Rn．

（1）写出上述衰变方程；
（2）若A处距磁场边界MN的距离OA=1.0m时，放在MN左侧边缘的粒子接收器收到垂直于边界MN方向射出的质量较小的粒子，此时接收器距过OA的直线1.0m．求一个静止 Ra核衰变过程中释放的核能有多少？（取1u=1.6×10﹣27 kg，e=1.6×10﹣19 C，结果保留三位有效数字）

Answer 1

【答案】
（1）解：根据质量数与质子数守恒，可得衰变的方程：

Ra→ Rn+ He；

答：衰变方程 Ra→ Rn+ He；

（2）解：衰变过程中释放的α粒子在磁场中做匀速圆周运动，半径R=1.0 m，由2evB= 得

α粒子的速度v=

衰变过程中系统动量守恒， Rn、 He质量分别为222 u、4 u，则

222 u×v′=4 u×v

得 Rn的速度v′= v

释放的核能E= ×222 u×v′2+ ×4 u×v2=

代入数据解得E=2.04×10﹣14 J．

答：一个静止 Ra核衰变过程中释放的核能有2.04×10﹣14 J．

【解析】（1）根据质量数与质子数守恒，写出衰变方程；（2）由于粒子做匀速圆周运动，根据牛顿第二定律，可算出运动轨迹的半径；从而可确定粒子的动量及动能．再根据动量守恒定律，从而即可求解．