题目内容
【题目】如图所示，在空间XOY的第一象限内存在一沿-X轴方向，大小为E的匀强电场。现有一质量为m，电量为＋q的带电微粒（重力不计），在A（L，L）点无初速度释放，通过Y轴上的P点进入第二象限，在第二象限内存在沿-Y轴方向匀强电场，带电微粒最终从C（0，-2L）点离开第二象限。
（1）则第二象限内场强大小？带电微粒从C点离开的速度是多少？
（2）若第二象限内仅存在沿垂直纸面的匀强磁场，使带电微粒仍从C（0，-2L）点离开，则磁感应强度大小？
若改变带电微粒释放点的位置从P点进入磁场，在第二象限有垂直纸面的圆形匀强磁场，使得粒子从C点离开的速度与只在电场时完全相同，则第二象限内圆形匀强磁场的磁感应强度是多少？圆形匀强磁场的面积是多少？
【答案】（1）E 
（2）
(3) 
【解析】试题分析：画出粒子运动轨迹，根据动能定理得和平抛公式结合即可解题；做圆周运动到达C点，根据洛伦兹力提供向心力结合几何关系即可求出磁感应强度大小；因在磁场中速度大小不变，故改变带电微粒释放点的位置到P点时速度已经达到vc，画出粒子运动轨迹，根据洛伦兹力提供向心力结合几何知识即可求出磁感应强度和圆形匀强磁场的面积。
（1）粒子运动轨迹如图所示：
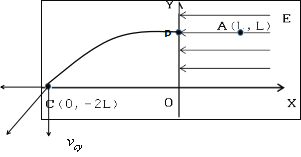
在第一象限内：根据动能定理得： 
进入第二象限，在水平方向： 
在竖直方向： 
加速度为： 
联立可得： 
在C点的竖直速度为： 
水平速度为： 
联立可得： 
方向与-x轴夹角450
（2）做圆周运动到达C点，如图所示：
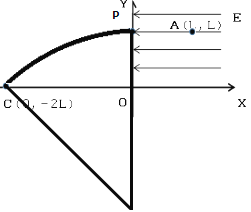
半径满足： 
解得： 
根据洛伦兹力提供向心力： 
可得： 
（3）因在磁场中速度大小不变，故改变带电微粒释放点的位置到P点时速度已经达到： 
要使磁感应强度B最小，则半径最大，如图所示：
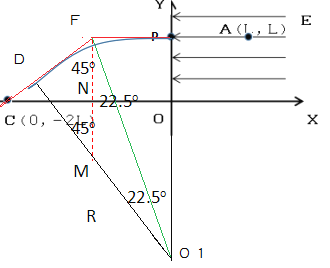
粒子进入第二象限时就进入磁场，从D点离开，过C点速度的反向沿长线过水平位移的中点，由几何关系有， 
， 
所以轨迹半径： 
根据洛伦兹力提供向心力： 
所以可得：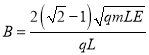 
圆形磁场的半径为
，所以
所以面积为： 
