Question

【题目】将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体，其截面的正视图如图所示，MNPQ为其底面（PQ图中未画出），MN为直径．已知半圆的圆心为O、半径为R，玻璃的折射率n= ．一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上，经折射后，有部分光能从MNPQ面射出，忽略经多次反射到达MNPQ面的光线，求MNPQ透光部分的面积．

Answer 1

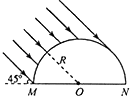
【答案】解：设光由介质射向空气的临界角为C．
由 sinC= ，得 C=45°
从A点进入玻璃砖的光线垂直半球面，沿半径AO直达球心O，且入射角等于临界角，恰好在O点发生全反射，A点左侧的光线经球面折射后，射在MN上的入射角都大于临界角，在MN上全反射，不能从MN上射出．A点右侧光线一直到与球面正好相切的范围内的光线经球面折射后，在MN上的入射角均小于临界角，都能从MN上射出，它们在MN上的出射宽度就是OD．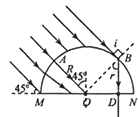

由折射定律得
=n
MN上透光部分的长度：
OD=Rsinr
MNPQ平面内透光部分面积为：
S=ODl= Rl
答：MNPQ透光部分的面积为 Rl．
【解析】光线射到MN上时会发生全反射现象，从而不能从MN射出；根据临界角公式sinC= 求出临界角C，根据几何关系确定能从MN射出的光线范围，由几何知识求解面积．
【考点精析】通过灵活运用光的折射，掌握光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射即可以解答此题．