题目内容
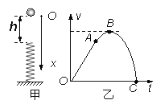
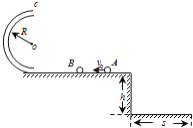
【题目】如图所示,光滑水平轨道距地面高h=0.8m,其左端固定有半径R=0.6m的内壁光滑的半圆管形轨道,轨道的最低点和水平轨道平滑连接.质量m1=1.0kg的小球A以v0=9m/s的速度与静止在水平轨道上的质量m2=2.0kg的小球B发生对心碰撞,碰撞时间极短,小球A被反向弹回并从水平轨道右侧边缘飞出,落地点到轨道右边缘的水平距离s=1.2m.重力加速度g=10m/s2.求:
(1)碰后小球B的速度大小vB;
(2)小球B运动到半圆管形轨道最高点C时对轨道的压力.
【答案】(1)6m/s(2)20N,向下
【解析】
(1)根据![]()
得:![]()
则![]()
规定A的初速度方向为正方向,AB碰撞过程中,系统动量守恒,以A运动的方向为正方向,有:m1v0=m2vB-m1vA,
代入数据解得:vB=6m/s.
(2)根据动能定理得:![]()
代入数据解得:![]()
根据牛顿第二定律得:![]()
解得:![]() ,方向向下
,方向向下
根据牛顿第三定律得,小球对轨道最高点的压力大小为20N,方向向上.

练习册系列答案
相关题目