题目内容
【题目】兔子在雪地奔跑，狗拉雪橇的猎人紧追不舍，如果拉雪橇的绳子突然断了会是怎样一副场景。如图所示（把猎人和雪橇看成一个金属块），质量为2kg的金属块放在水平地面上，在大小为20N、方向与水平方向成37°角的斜向上拉力F作用下，从静止开始做匀加速直线运动.已知金属块与地面间的动摩擦因数μ=0.5，力F持续作用2s后撤去。（g取10m/s2）.
求：
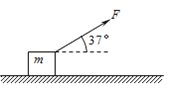
（1）力F撤去的瞬间金属块的速度为多大？
（2）金属块在地面上总共滑行了多远？
【答案】(1)12m/s(2)26.4m
【解析】试题分析：对金属块受力分析后，根据牛顿第二定律列式求解加速度，根据速度时间公式求金属块的速度；根据位移时间关系公式列式求出撤去F前金属块的位移；撤去F后，再根据牛顿第二定律求解出加速度，再根据速度位移公式求解位移．
（1）金属块受力如下图所示．
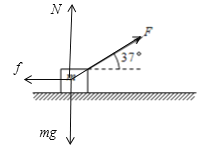
根据牛顿第二定律得：
水平方向
，竖直方向： 
，其中
得
，解得
撤去F瞬间，金属块的速度
（2）撤去F前金属块的位移
撤去力F后金属块的加速度大小
由
，代入数据解得
则金属块在地面上总共滑行了
．
练习册系列答案
相关题目
