题目内容
过山车是游乐场中常见的设施。如图是一种过山车的简易模型，它由水平轨道和在竖直平面内半径R= 2.0m的圆形轨道组成，B、C分别是圆形轨道的最低点和最高点。一个质量为m=1.0kg的小滑块（可视为质点），从轨道的左侧A点以v0= 12m/s的初速度沿轨道向右运动，A、B间距L= 11.5m。小滑块与水平轨道间的动摩擦因数
。圆形轨道是光滑的，水平轨道足够长。取重力加速度g=10m/s2。求：
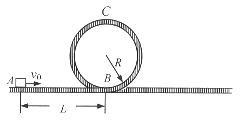
（1）滑块经过B点时的速度大小
;
（2）滑块经过C点时受到轨道的作用力大小F；
（3）滑块最终停留点D（图中未画出）与起点A的距离d。
（1）11m/s；（2）10.5N；（3）72m
解析试题分析:从A到B，根据动能定理得：?μmgL＝
①
代入数据解得：vB=11m/s
（2）从B到C，根据机械能守恒得：
；
小滑块在最高点受到重力mg和轨道对它的作用力F，根据牛顿第二定律有：
代入数据解得：F=10.5N；
（3）小滑块在整个运动的过程中，摩擦力做功与小滑块动能的变化．
得：?μmgx＝0?
得：x＝72m；
考点：动能定理；牛顿第二定律；机械能守恒定律
练习册系列答案
相关题目
，上表面光滑，小车与地面间的摩擦力极小，可以忽略不计。可视为质点的物块B置于A的最右端，B的质量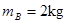
。现对A施加一个水平向右的恒力F＝10N，A运动一段时间后，小车左端固定的挡板B发生碰撞，碰撞时间极短，碰后A、B粘合在一起，共同在F的作用下继续运动，碰撞后经时间t＝0.6s，二者的速度达到
。求
由
板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区。当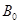
和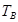
取某些特定值时，可使
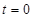时刻入射的粒子经
时间恰能垂直打在
板上（不考虑粒子反弹）。上述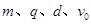
为已知量。
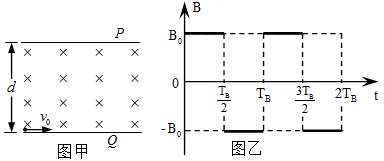
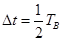，求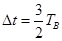
，求粒子在磁场中运动时加速度的大小； 
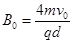，为使粒子仍能垂直打在
＝7m/s的初速从左侧磁场边缘水平进入磁场，求：
。（取g=10m／s2）求：
