题目内容
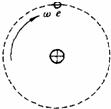 电子在匀强磁场中以某固定的正电荷为中心做顺时针方向的匀速圆周运动,如图所示.磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷与电子的带电量均为e,电子质量为m,圆周半径为r,则下列判断中正确的是( )
电子在匀强磁场中以某固定的正电荷为中心做顺时针方向的匀速圆周运动,如图所示.磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷与电子的带电量均为e,电子质量为m,圆周半径为r,则下列判断中正确的是( )分析:电子做匀速圆周运动,靠库伦引力和洛伦兹力的合力提供向心力,根据牛顿第二定律进行分析.
解答:解:A、如果k
<Bev,因为库伦引力指向圆心,则洛伦兹力一定指向圆心,根据左手定则,磁感线一定指向纸内.故A正确.
B、如果2k
=Bev,知洛伦兹力方向指向圆心,根据牛顿第二定律得,k
+Bev=mrω2,解得ω=
.故B正确.
C、如果k
>Bev,洛伦兹力的方向可能指向圆心,可能背离圆心,做匀速圆周运动,所以角速度可能有两个值.故C错误,D正确.
故选ABD.
| e2 |
| r2 |
B、如果2k
| e2 |
| r2 |
| e2 |
| r2 |
| 3Be |
| 2m |
C、如果k
| e2 |
| r2 |
故选ABD.
点评:解决本题的关键知道电子做匀速圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
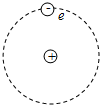 如图所示,电子在匀强磁场中以某固定的正电荷为中心做顺时针方向的匀速圆周运动,磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷与电子的带电量绝对值均为e,电子质量为m,圆周半径为r,静电力常量为k,电子的重力忽略不计,则下列判断中正确的是( )
如图所示,电子在匀强磁场中以某固定的正电荷为中心做顺时针方向的匀速圆周运动,磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷与电子的带电量绝对值均为e,电子质量为m,圆周半径为r,静电力常量为k,电子的重力忽略不计,则下列判断中正确的是( )A、如果k
| ||||
B、如果2k
| ||||
C、如果k
| ||||
D、如果k
|
 电子在匀强磁场中以某固定的正点电荷为中心作顺时针方向的匀速圆周运动,如图所示.磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷和电子的电量均为e,电子的质量为m,圆周半径为r,则下列说法正确的是
电子在匀强磁场中以某固定的正点电荷为中心作顺时针方向的匀速圆周运动,如图所示.磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷和电子的电量均为e,电子的质量为m,圆周半径为r,则下列说法正确的是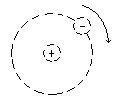 电子在匀强磁场中以某固定的正点电荷为中心作顺时针方向的匀速圆周运动,如图所示.磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷和电子的电量均为e,电子的质量为m,圆周半径为r,则下列说法正确的是
电子在匀强磁场中以某固定的正点电荷为中心作顺时针方向的匀速圆周运动,如图所示.磁场方向与电子运动平面垂直,磁感应强度为B,电子速率为v,正电荷和电子的电量均为e,电子的质量为m,圆周半径为r,则下列说法正确的是