题目内容

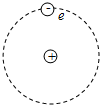精英家教网如图所示，电子在匀强磁场中以某固定的正电荷为中心做顺时针方向的匀速圆周运动，磁场方向与电子运动平面垂直，磁感应强度为B，电子速率为v，正电荷与电子的带电量绝对值均为e，电子质量为m，圆周半径为r，静电力常量为k，电子的重力忽略不计，则下列判断中正确的是（　　）
A、如果k
e2
r2
＜Bev，则磁场方向一定指向纸内
B、如果2k
e2
r2
=Bev，则电子角速度为
3Be
2m
C、如果k
e2
r2
＞Bev，则磁场的方向可能指向纸外
D、如果k
e2
r2
＞Bev，则电子不能做匀速圆周运动
分析：电子做匀速圆周运动，靠库仑引力和洛伦兹力的合力提供向心力，根据牛顿第二定律进行分析即可．
解答：解：电子做匀速圆周运动，由库仑引力和洛伦兹力的合力提供向心力．
A、如果k
e2
r2
＜Bev，因为库仑引力指向圆心，则洛伦兹力一定指向圆心，根据左手定则，磁感线一定指向纸内．故A正确．
B、如果2k
e2
r2
=Bev，知洛伦兹力方向指向圆心，根据牛顿第二定律得：k
e2
r2
+Bev=mω2r，解得ω=
3Be
2m
．故B正确．
C、D如果k
e2
r2
＞Bev，则洛伦兹力的方向可能指向圆心，可能背离圆心，仍能做匀速圆周运动，所以磁场方向可能指向纸外，也可能指向纸内．故C正确，D错误．
故选：ABC．
点评：解决本题的关键知道电子做匀速圆周运动向心力的来源，知道匀速圆周运动由合外力充当向心力，再结合牛顿第二定律进行求解．
练习册系列答案
相关题目
如图所示，有一匀强电场，场强为E，方向与坐标平面Oxy平行，跟x轴的负方向夹角为θ，电子在坐标平面Oxy内，从原点O垂直于电场方向、以大小为v0的初速度射入第一象限．电子的质量为m，电荷量为e，重力不计．求：
（1）电子再次通过x轴时与O点的距离；
（2）从O点到再次通过x轴的过程中，电子电势能的改变量．
（2010?南通二模）如图所示，有界匀强磁场磁感应强度为B，方向垂直纸面向里，MN为其左边界，磁场中放置一半径为R的圆柱形金属圆筒，圆心O到MN的距离OO1=2R，圆筒轴线与磁场平行．圆筒用导线通过一个电阻r0接地，最初金属圆筒不带电．现有范围足够大的平行电子束以速度v0从很远处沿垂直于左边界MN向右射入磁场区，已知电子质量为m，电量为e．
（1）若电子初速度满足v0=
3eBRm
，则在最初圆筒上没有带电时，能够打到圆筒上的电子对应MN边界上O1两侧的范围是多大？
（2）当圆筒上电量达到相对稳定时，测量得到通过电阻r0的电流恒为I，忽略运动电子间的相互作用，求此时金属圆筒的电势φ和电子到达圆筒时速度v（取无穷远处或大地电势为零）．
（3）在（2）的情况下，求金属圆筒的发热功率．
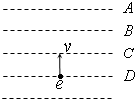精英家教网如图所示，有界匀强磁场的磁感应强度为B特斯拉，磁场方向垂直于纸面向里，MN是磁场的左边界．在磁场中A处放一个放射源内装
 
226
88
Ra（镭），
 
226
88
Ra放出某种射线后衰变成
 
222
86
Rn（氡），粒子可向各个方向射出．若A距磁场的左边界MN的距离OA=d 时，从A点沿垂直OA向上射出的质量较小粒子，恰好使放在MN左侧的粒子接收器接收到垂直于边界MN方向射出的该粒子，此时接收器位置距OA直线的距离也为d．由此可以推断出（取原子质量单位用m0表示，电子电量用e表示）．
（1）试写出
 
226
88
Ra衰变的方程且确定射出的质量较小的粒子在磁场中的轨迹圆半径是多少？
（2）射出的质量较小的粒子的速度为多少？
（3）这一个静止镭核
 
226
88
Ra衰变时亏损质量多大？（提示：动量守恒定律在微观领域仍适用，系统增加机械能来自核能释放）?
精英家教网如图所示，ABCD为匀强电场中相邻的四个等势面，相邻等势面间距离为5cm．一个电子仅受电场力垂直经过电势为零的等势面D时，动能为15eV（电子伏），到达等势面A时速度恰好为零．则下列说法正确的是（　　）
A、场强方向从A指向DB、匀强电场的场强为100 V/mC、电子经过等势面C时，电势能大小为5 eVD、电子在上述等势面间运动的时间之比为1：2：3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

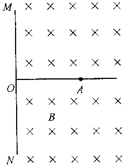精英家教网