题目内容
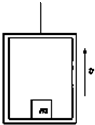 如图所示,电梯质量为M,地板上放置一质量为m的物体.钢索拉电梯由静止开始向上加速运动,当上升高度为H时,速度达到v,则( )
如图所示,电梯质量为M,地板上放置一质量为m的物体.钢索拉电梯由静止开始向上加速运动,当上升高度为H时,速度达到v,则( )A、地板对物体的支持力做的功等于
| ||||
B、地板对物体的支持力做的功等于
| ||||
C、钢索的拉力做的功等于
| ||||
D、合力对电梯M做的功等于
|
分析:根据电梯的运动情况,可以求得电梯的加速度的大小,再有牛顿第二定律可以求得电梯对物体的支持力的大小,从而可以求得功的大小.
解答:解:电梯由静止开始向上做加速运动,设加速度的大小为a,
由速度和位移的关系式可得,v2=2aH,
所以a=
,
对电梯由牛顿第二定律可得,
FN-mg=ma,
所以 FN=mg+ma=mg+m
,
地板对物体的支持力做的功为W=FNH=(mg+ma)H=mgH+
mv2,所以A错误,B正确.
对于整体由牛顿第二定律可得,
F-(M+m)g=(M+m)a,
所以钢索的拉力为F=(M+m)g+(M+m)a,
钢索的拉力做的功等于FH=(M+m)gH+
(M+m)v2,所以C错误.
根据动能定理可得,合力对电梯M做的功等于电梯的动能的变化即为
Mv2,所以D错误.
故选:B.
由速度和位移的关系式可得,v2=2aH,
所以a=
| v2 |
| 2H |
对电梯由牛顿第二定律可得,
FN-mg=ma,
所以 FN=mg+ma=mg+m
| v2 |
| H |
地板对物体的支持力做的功为W=FNH=(mg+ma)H=mgH+
| 1 |
| 2 |
对于整体由牛顿第二定律可得,
F-(M+m)g=(M+m)a,
所以钢索的拉力为F=(M+m)g+(M+m)a,
钢索的拉力做的功等于FH=(M+m)gH+
| 1 |
| 2 |
根据动能定理可得,合力对电梯M做的功等于电梯的动能的变化即为
| 1 |
| 2 |
故选:B.
点评:解决本题的关键是对物体的受力分析,再根据功的公式可以逐个来求得每个力的功.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示,电梯质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动,当上升高度为H时,电梯的速度达到v,则在这段过程中,以下说法正确的是( )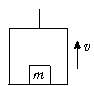
A.电梯地板对物体的支持力所做的功等于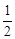 mv2 mv2 |
B.电梯地板对物体的支持力所做的功大于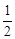 mv2 mv2 |
C.钢索的拉力所做的功等于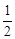 Mv2+MgH Mv2+MgH |
D.钢索的拉力所做的功大于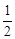 Mv2+MgH Mv2+MgH |
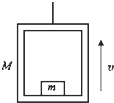 如图所示,电梯质量为M,地板上放置一质量为m的物体,钢索拉着电梯由静止开始向上做加速运动,当上升高度为H时,速度达到v,则( )
如图所示,电梯质量为M,地板上放置一质量为m的物体,钢索拉着电梯由静止开始向上做加速运动,当上升高度为H时,速度达到v,则( )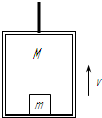 如图所示,电梯质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动,当上升高度为H时,电梯的速度达到v,则在这个过程中( )
如图所示,电梯质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动,当上升高度为H时,电梯的速度达到v,则在这个过程中( )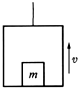 如图所示,电梯质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动.当上升高度为H时,电梯的速度达到v,则在这段过程中,下列说法中正确的是( )
如图所示,电梯质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动.当上升高度为H时,电梯的速度达到v,则在这段过程中,下列说法中正确的是( )