题目内容
【题目】重10N的滑块在倾角为30°的光滑斜面上，从a点由静止下滑，到b点接触到一个轻弹簧，滑块压缩弹簧到c点开始弹回，返回b点离开弹簧，最后又回到a点，已知ab=1m，bc=0.2m，那么在整个过程中（ ）
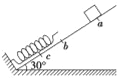
A. 滑块经过B点时动能最大
B. 弹簧弹性势能的最大值是6 J
C. 从c到b弹簧的弹力对滑块做的功是6 J
D. 整个过程滑块的机械能守恒
【答案】BC
【解析】滑块向下滑动刚刚接触b点时，弹簧处于原长，在弹力不大于重力平行斜面分力时，滑块一直在加速，故b点速度不是最大，动能也就不是最大，故A错误；在c点，弹簧压缩量最大，故弹性势能最大，对从a到c过程，根据功能关系，有：
Ep=mg（ab+ac）sin30°=10×（1+0.2）×
=6J；故B正确；从c到b弹簧的弹力对滑块做的功等于其弹性势能的减小量，为：W=Ep=6J，故C正确；整个过程中弹簧、滑块组成的系统机械能守恒，滑块的机械能不守恒，故D错误；故选BC.
练习册系列答案
相关题目
