Question

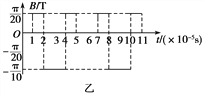
【题目】如图甲所示，水平直线MN上方有竖直向下的匀强电场，场强大小E＝π×103 N/C，MN下方有垂直于纸面的磁场，磁感应强度B随时间t按如图乙所示规律做周期性变化，规定垂直纸面向外为磁场正方向．T＝0时将一重力不计、比荷＝106 C/kg的正点电荷从电场中的O点由静止释放，在t1＝1×10－5 s时恰通过MN上的P点进入磁场，P点左方d＝105 cm处有一垂直于MN且足够大的挡板．求：

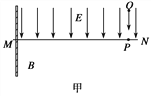
(1)电荷从P点进入磁场时速度的大小v0；

(2)电荷在t2＝4×10－5 s时与P点的距离Δx；

(3)电荷从O点出发运动到挡板所需时间t总．

Answer 1

【答案】(1)π×104 m/s　(2)20cm　(3)1.42×10－4 s

【解析】

(1)电荷在电场中做匀加速直线运动，则

Eq＝ma

v0＝at1

解得

v0＝＝π×103×106×1×10－5 m/s＝π×104 m/s

(2)电荷在磁场中做匀速圆周运动，洛伦兹力提供向心力

qvB＝m，r＝

当B1＝T时，

半径

r1＝＝0.2 m＝20 cm

周期

T1＝＝4×10－5 s

当B2＝T时，半径

r2＝＝0.1 m＝10 cm

周期

T2＝＝2×10－5 s

故电荷从t＝0时刻开始做周期性运动，其运动轨迹如图所示．

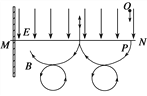
在t＝0到t2＝4×10－5 s时间内，电荷先沿直线OP运动t1，再沿大圆轨迹运动，紧接着沿小圆轨迹运动T2，t2＝4×10－5 s时电荷与P点的距离

Δx＝r1＝20 cm

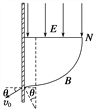
(3)电荷从P点开始的运动周期T＝6×10－5 s，且在每一个周期内向左沿PM移动x1＝2r1＝40 cm，电荷到达挡板前经历了2个完整周期，沿PM运动距离x＝2x1＝80 cm，设电荷撞击挡板前速度方向与水平方向成θ角，最后d－x＝25 cm内的轨迹如图所示．

据几何关系有

r1＋r2sin θ＝0.25 m

解得

sin θ＝0.5，

即θ＝30°

则电荷从O点出发运动到挡板所需总时间

t总＝t1＋2T＋

解得

t总＝×10－5 s≈1.42×10－4 s.