Question

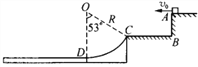
【题目】被截去1/4的圆形轨道与直轨道相切于A点，整个轨道固定在水平桌面上，空间足够大范围存在匀强电场, 场强大小为E，方向与直轨道成θ=37°夹角，俯视图如图。质量为m，电量为q的带正电小球紧贴桌面，靠着轨道某点P静止释放，轨道与桌面绝缘和光滑，圆轨道半径为R。已知sin37°=0.6，cos37°=0.8。求：

(1)若PA=R，小球刚进入圆轨道时对轨道的压力大小；

(2)改变释放点P与A的距离，使小球能沿着轨道运动到D点，则小球经过A点时的速度至少多大。

Answer 1

【答案】(1)2.2qE；(2)

【解析】

(1)从P到A由动能定理可知：

在A点由牛顿第二定律可得：

解得：

由牛顿第三定律可知，小球对轨道的压力为2.2qE；

(2)由“等效重力”可知，要使小球能运动到D点，即小球能过“等效重力场”的最高点M，如图所示

在最高点M，只有电场力提供向心力

从A到M，轨道固定在水平桌面上，小球在水平面上运动 ，只有电场力做功，由动能定理可得：

解得