题目内容
【题目】如图所示，一质量M=0.4kg的滑块放在光滑水平面上处于静止状态，滑块左侧为一光滑的 
圆弧，水平面恰好与圆弧相切．质量m=0.1kg的小球（视为质点）以v0=5m/s的初速度向右运动冲上滑块．取g=10m/s2 ． 若小球刚好没有冲出 圆弧的上端，求：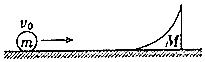
（1）小球上升到滑块上端时的速度大小；
（2） 圆弧的半径；
（3）滑块获得的最大速度．
【答案】
（1）解：当小球上升到滑块上端时，小球与滑块水平方向速度相同，设为v1，以水平向右为正方向，在水平方向上，由动量守恒定律得：
mv0=（m+M）v1
代入数据得：v1=1m/s
答：小球上升到滑块上端时的速度大小是1m/s；
（2）解：由机械能守恒定律得： 
mv02= （m+M）v12+mgR
代入数据解得圆弧的半径为：R=1m
答： 
圆弧的半径是1m；
（3）解：小球到达最高点以后又滑回，滑块仍做加速运动，当小球离开滑块时滑块速度最大．研究小球开始冲上滑块一直到离开滑块的整个过程，以水平向右为正方向，由动量守恒定律得：
mv0=mv2+Mv3
由机械能守恒定律得： mv02= mv22+ Mv32
解得：v3= 
= 
=2m/s
答：滑块获得的最大速度是2m/s．
【解析】本题综合应用了动量守恒定律和机械能守恒定律，对两个定律的异同点要有深刻的理解，并清楚每个定律应该怎么用。
【考点精析】通过灵活运用机械能守恒及其条件和动量守恒定律，掌握在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变；动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变即可以解答此题．
