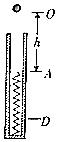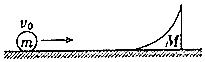��Ŀ����
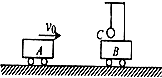
����Ŀ���ڡ�̽�������ٶȱ仯�Ĺ�ϵ��ʵ���У�������ͼ����ʾװ�ã�ˮƽ����������������߶�Ϊh������Ƥ������˹̶������ӱ�Ե�ϵ����㣬��С��������Ƥ����е㣬�����ƶ�����s��ʹ��Ƥ������α䣬�ɾ�ֹ�ͷź�С��������棬�����ƽ��ˮƽ���ΪL���ı���Ƥ����������ظ�ʵ�飮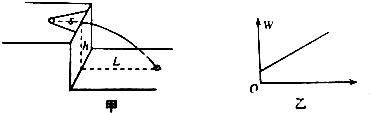
��1��ʵ���У�С��ÿ���ͷŵ�λ�õ����ӱ�Ե�ľ���sӦ����ͬ����ͬ�����⣩
��2��ȡ��Ƥ���С������WΪ�����꣬Ϊ��������ϵ�����õ�һ��ֱ�ߣ���ͼ����ʾ��ӦѡΪ�����꣨ѡL��L2����������������Ľؾ�Ϊb��б��Ϊk������С���������Ķ�Ħ������Ϊ��ʹ�������������ű�ʾ����
���𰸡�
��1����ͬ
��2��L2��![]()
���������⣺��1��С��ÿ���ͷŵ�λ�õ����ӱ�Ե�ľ���sҪ��ͬ��������֤ÿ����Ƥ�����α�����ȣ���ÿ�����ɵ������Ĺ���ȣ���2��С���׳�����ƽ���˶�������h= ![]() ����ã�t=
����ã�t= ![]() ������ٶ�
������ٶ� ![]() ��
��
���ݶ��ܶ����ã�W����mgs= ![]() ��
��
��W= ![]() +��mgs
+��mgs
����ӦѡL2Ϊ�����꣬б��k= ![]() ��b=��mgs
��b=��mgs
����= ![]()
���Դ��ǣ���1����ͬ����2��L2�� ![]()

��ϰ��ϵ�д�
�����Ŀ