题目内容
(9分)如图所示,质量为m=lkg的小物块由静止轻轻放在水平匀速运动的传送带上,从A点随传送带运动到水平部分的最右端B点,经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道,恰能做圆周运动。C点在B点的正上方,D点为轨道的最低点。小物块离开D点后,做平抛运动,恰好垂直于倾斜挡板打在挡板跟水平面相交的E点。已知半圆轨道的半径R=0.9 m,D点距水平面的高度h =0.75 m,取g="10" m/s2,试求: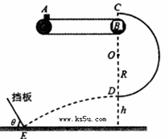
(1)摩擦力对物块做的功;
(2)小物块经过D点时对轨道压力的大小;
(3)倾斜挡板与水平面间的夹角θ。
(1)4.5J (2) 60N (3) 60°
解析试题分析:(1)设小物块经过C点时的速度大小为v1,经过C点恰能做圆周运动,所以,由牛顿第二定律得:
mg=mv12/R
解得v1=3m/s
小物块由A运动到B的过程中,设摩擦力对小物块做的功为w,由动能定理得:
W=mv12/2=4.5J
(2)设小物块经过D点时的瞬时速度大小为v2,对由C点运动到D点的过程,有机械能守恒定律得:
mv12/2+mg2R=mv22/2
小物块经过D点时,设轨道对它的支持力大小为FN,由牛顿第二定律得:
FN-mg=mv22/R
联立解得:FN=60N
由牛顿第三定律可知,小物体对轨道的压力大小为:
FN’=FN=60N
(3)小物块离开D点后做平抛运动,设经时间t打在E点,由h=gt2/2
t= s
s
设小物块打在E点时速度的水平、竖直分量分别为vx、vy,速度与竖直方向夹角为a,则
Vx=v2
Vy=gt
tana= Vx/ Vy
tana= 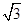
a=60°
由几何关系得:θ=a=60°
考点:本题考查牛顿第二定律、动能定理、机械能守恒定律、平抛运动。

练习册系列答案
相关题目
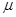 =0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
=0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求: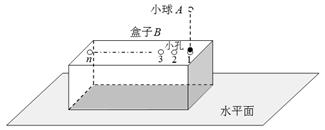
 =30°,皮带在电动机的带动下,始终保持顺时针运行,速率为v0=2m/s。现把一质量m=10kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:(1)工件与皮带间的动摩擦因数;(2)电动机由于传送工件多消耗的电能。
=30°,皮带在电动机的带动下,始终保持顺时针运行,速率为v0=2m/s。现把一质量m=10kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:(1)工件与皮带间的动摩擦因数;(2)电动机由于传送工件多消耗的电能。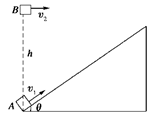
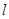 时,装置可安全工作。 一质量为m 的小车若以速度
时,装置可安全工作。 一质量为m 的小车若以速度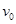 撞击弹簧,可使轻杆向右移动了
撞击弹簧,可使轻杆向右移动了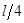 。轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦。
。轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦。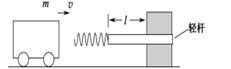
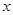
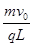 、方向垂直纸面向外的匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,–
、方向垂直纸面向外的匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,– L)的A点以速度v0沿+x方向射出,恰好经过坐标为[0,-(
L)的A点以速度v0沿+x方向射出,恰好经过坐标为[0,-(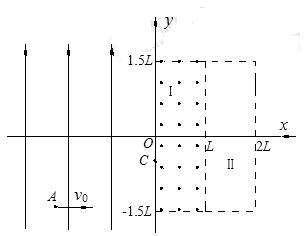
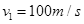 ,飞行员对机座的压力恰好为零,则轨道半径R= m,若飞机飞到最低点时速度为
,飞行员对机座的压力恰好为零,则轨道半径R= m,若飞机飞到最低点时速度为 ,飞行员对机座的压力N= N。
,飞行员对机座的压力N= N。
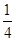 圆弧AB,半径
圆弧AB,半径 ,固定在竖直平面内。一辆质量为M=2kg的小车处在水平光滑平面上,小车的表面CD与圆弧在B点的切线重合,初始时B与C紧挨着,小车长L=1m,高H=0.2m。现有一个质量为m=1kg的滑块(可视为质点),自圆弧上的A点从静止开始释放,滑块运动到B点后冲上小车,带动小车向右运动,当滑块与小车分离时,小车运动了
,固定在竖直平面内。一辆质量为M=2kg的小车处在水平光滑平面上,小车的表面CD与圆弧在B点的切线重合,初始时B与C紧挨着,小车长L=1m,高H=0.2m。现有一个质量为m=1kg的滑块(可视为质点),自圆弧上的A点从静止开始释放,滑块运动到B点后冲上小车,带动小车向右运动,当滑块与小车分离时,小车运动了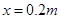 ,此时小车的速度为
,此时小车的速度为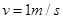 。求
。求