��Ŀ����
18��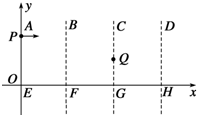 ��ͼ��ʾ����ֱƽ��xOy�����������Ⱦ�ΪL��β��ӵĵ糡����ABFE��BCGF��CDHG�����������зֱ���ڷ���Ϊ+y��+y��+x����ǿ�糡���䳡ǿ��С����Ϊ2��1��2������һ�������������ijһ���ٶȴ�����Ϊ��0��L����P������ABFE���������ٶȷ���ˮƽ���ң�����ǡ������Ϊ��2L��$\frac{L}{2}$����Q������CDHG��������֪������ABFE�������ܵ糡��������������С��ȣ��������ٶ�Ϊg�����������Ϊ�ʵ㣬y����ֱ���ϣ���������ֱ����糡�㹻����
��ͼ��ʾ����ֱƽ��xOy�����������Ⱦ�ΪL��β��ӵĵ糡����ABFE��BCGF��CDHG�����������зֱ���ڷ���Ϊ+y��+y��+x����ǿ�糡���䳡ǿ��С����Ϊ2��1��2������һ�������������ijһ���ٶȴ�����Ϊ��0��L����P������ABFE���������ٶȷ���ˮƽ���ң�����ǡ������Ϊ��2L��$\frac{L}{2}$����Q������CDHG��������֪������ABFE�������ܵ糡��������������С��ȣ��������ٶ�Ϊg�����������Ϊ�ʵ㣬y����ֱ���ϣ���������ֱ����糡�㹻������1���������ABFE����ʱ�ij��ٶȴ�С��
��2�������Y�����糡������X��ʱ��������ʱ�䣻
��3�������DH�߽����λ�õ����꣮
���� ��1���������������������˶������������ABFE�������ܵ糡��������������С��ȣ�������ֱ���˶�������BCGF��������ֱ���µ���������ֱ���ϵĵ糡��������ƽ���˶����������嵽��Q���ٶȴ�С�ͷ������������CDHG���˶��������BCDF������������ƽ���˶���ˮƽλ��ΪL����ֱλ��Ϊ$\frac{L}{2}$������ţ�ٵڶ�����������ٶȣ������˶��ķֽⷽ����������ٶȣ�
��2��������ABFE����������ֱ���˶�������λ�ƺͳ��ٶ����ʱ�䣻��BCGF������������ƽ���˶���������嵽��Q�ٶȴ�С�ͷ����������CDHG�������ȼ���ֱ���˶�����ţ�ٵڶ����ɺ�λ�ƹ�ʽ������ʱ�䣬�������ʱ�䣮
��3�������DH�߽����ʱ������Ϊ3L������������������������ֱ�����ƫ��������������꣮
��� �⣺����������ĵ糡ǿ�ȴ�С����Ϊ2E��E��2E�����������������˶���ʱ��ֱ�t1��t2��t3��
��1����BCGF�����������������������ţ�ٵڶ����ɵã�
mg-qE=ma2��
����2qE=mg
�ã�a2=$\frac{g}{2}$
��ˮƽ�����У�L=v0t
����ֱ�����У�$\frac{L}{2}$=$\frac{1}{2}$a2${t}_{2}^{2}$
��ã�v0=$\sqrt{\frac{gL}{2}}$��t2=$\sqrt{\frac{2L}{g}}$
��2����ABEF�������������������������ֱ�����У�2qE=mg
����������ֱ���˶����У�v0=$\sqrt{\frac{gL}{2}}$��t1=t2=$\sqrt{\frac{2L}{g}}$
��BCGF������������ƽ���˶����У�v0=$\sqrt{\frac{gL}{2}}$��t2=$\sqrt{\frac{2L}{g}}$
��Q����ֱ�����ٶ�Ϊ��vy=a2t2=$\sqrt{\frac{gL}{2}}$=v0��
��Q���ٶ�Ϊ��vQ=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{gL}$����ˮƽ����н�Ϊ45��
��CDHG���� ����2qE=mg
�������������������F=$\sqrt{2}$mg����ˮƽ����н�Ϊ45�㣬���ٶȷ�����ͬ���������ȼ���ֱ���˶���
�˶���X����̣������˶�ѧ��ʽ���У�$\frac{\sqrt{2}L}{2}$=vQt3+$\frac{1}{2}$a3${t}_{3}^{2}$
��ã�t3=��2-$\sqrt{2}$��$\sqrt{\frac{L}{g}}$
������t=t1+t2+t3=��2+$\sqrt{2}$��$\sqrt{\frac{L}{g}}$
��3��������ABFE����������ֱ���˶�����BCGF������������ƽ���˶���ƫ����Ϊ$\frac{L}{2}$��
��CDHG��������ˮƽ����н�Ϊ45�㣬�������ȼ���ֱ���˶�����ֱ����λ��ΪL���������DH�߽����λ�õ�����Ϊ��3L��-$\frac{L}{2}$����
�𣺣�1���������ABFE����ʱ�ij��ٶȴ�СΪ$\sqrt{\frac{gL}{2}}$��
��2��������ADHE�����˶�����ʱ��ΪΪ��2+$\sqrt{2}$��$\sqrt{\frac{L}{g}}$��
��3�������DH�߽����λ�õ�����Ϊ��3L��-$\frac{L}{2}$����
���� �����Ǵ������ڵ糡���������ĸ��ϳ����˶������⣬�ؼ��Ƿ������������������˶��������ƽ���˶������˶��ĺϳ���ֽ�ķ����о����ȼ���ֱ���˶�����ţ�ٶ��ɺ��˶�ѧ��ʽ����о���

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ͼ��ʾ�����㹻�ߵ�ͬһˮƽֱ����A��B��������ˮƽ�׳�����С������ij��ٶȷֱ�Ϊv1��v2���˶��켣��ͼ��ʾ��AO��BO�����ƿ���������������˵����ȷ���ǣ�������
��ͼ��ʾ�����㹻�ߵ�ͬһˮƽֱ����A��B��������ˮƽ�׳�����С������ij��ٶȷֱ�Ϊv1��v2���˶��켣��ͼ��ʾ��AO��BO�����ƿ���������������˵����ȷ���ǣ�������| A�� | ���ٶ�v1��v2 | |
| B�� | ������ͬʱ�׳���������һ������ | |
| C�� | ��A���׳���B���׳���������������� | |
| D�� | ������������������׳��������Ĺ�����������ٶȱ仯��ͬ |
| A�� | ��ǰ�㵹 | B�� | ����㵹 | ||
| C�� | ��ת�������㵹 | D�� | ��ת����ڲ��㵹 |

��1�����ʱ����������ʱ�����������ȡ����B
A�� ������ѹ�ĸߵ� B�� �������Ƶ�� C�� ī��ֽ�̵Ĵ�С�� D�� ֽ���ij���
��2�����ݴ���ʱ�������ֽ�������ǿ���ֱ�ӵõ�����������A
A��ʱ���� B�����ٶ� C��˲ʱ�ٶ� D��ƽ���ٶ�
��3������ֽ���ϸ����������ľ��룬ijͬѧ�ѽ�1��2��3��5���Ӧ��ʱ�̵�˲ʱ�ٶȽ��м��㲢������У����㽫4���Ӧ��ʱ�̵�˲ʱ�ٶ�������У���Ҫ����3λ��Ч���֣�
| ˲ʱ�ٶ� | v1 | v2 | v3 | v4 | v5 |
| ��ֵ��m/s�� | 0.165 | 0.214 | 0.263 | 0.363 |
��5����ͼ�����С���ļ��ٶ�a=0.5m/s2��Ҫ����1λ��Ч���֣�������ij��ʵ���У��������Ƶ��ƫ��50Hz����f��50Hz��������ļ��ٶ�ֵ����ʵֵ�����ƫС�v��ƫ����Ȼ�ƫС����
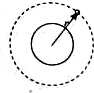
 �ڰ뾶Ϊr��Բ�οռ�����һ��ǿ�ų���һ�����������ٶ�v��A�ذ뾶�������䣬����C���������ͼ��ʾ��OΪԲ�ģ�����֪��AOC=120�㣬���ڴų�������ֻ�������������ã��������ڴų������е�ʱ�䣨������
�ڰ뾶Ϊr��Բ�οռ�����һ��ǿ�ų���һ�����������ٶ�v��A�ذ뾶�������䣬����C���������ͼ��ʾ��OΪԲ�ģ�����֪��AOC=120�㣬���ڴų�������ֻ�������������ã��������ڴų������е�ʱ�䣨������| A�� | $\frac{2��r}{3v}$ | B�� | $\frac{2\sqrt{3}��r}{3v}$ | C�� | $\frac{��r}{3v}$ | D�� | $\frac{\sqrt{3}��r}{3v}$ |
 ��ͼ��ʾ����֪�����Ƶ���ת�������ٶ�v������뾶Ϊr����������ΪG����
��ͼ��ʾ����֪�����Ƶ���ת�������ٶ�v������뾶Ϊr����������ΪG����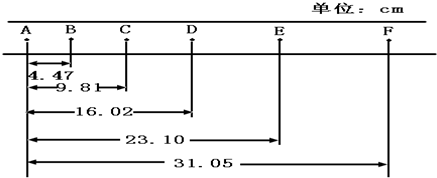
 ��ͼ��ʾ��һ����ΪL����Ϊm�Ľ�����ˮƽ�̶�������������ϵ����Ϊk�ĵ����ϣ���һ��ǿ�ų�B������ֱֽ�������������ͨ�����ҵĵ���Iʱ�������쳤��x���ɴ˿ɵôŸ�Ӧǿ��B�Ĵ�С��$\frac{2k��x-mg}{IL}$����ͨ������ĵ���Iʱ����������$\frac{mg}{k}-��x$��
��ͼ��ʾ��һ����ΪL����Ϊm�Ľ�����ˮƽ�̶�������������ϵ����Ϊk�ĵ����ϣ���һ��ǿ�ų�B������ֱֽ�������������ͨ�����ҵĵ���Iʱ�������쳤��x���ɴ˿ɵôŸ�Ӧǿ��B�Ĵ�С��$\frac{2k��x-mg}{IL}$����ͨ������ĵ���Iʱ����������$\frac{mg}{k}-��x$��