题目内容
3.在探究小车速度随时间变化的规律的实验中,某同学在一次实验中得到一条纸带数据如图图中A、B、C、D、E、F为相邻的计数点,相邻计数点间的时间间隔T=0.1s.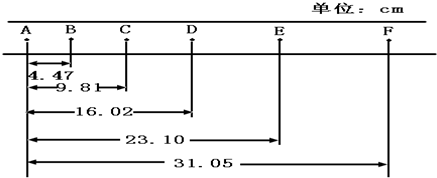
(1)根据纸带上的数据,算出B点的速度vB=0.49m/s,vD=0.66m/s
(2)根据纸带上的数据,小车运动加速度a=0.87m/s2.
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出B、D的瞬时速度,根据连续相等时间内的位移之差是一恒量,运用逐差法求出小车的加速度.
解答 解:(1)B点的瞬时速度${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{9.81×1{0}^{-2}}{0.2}m/s$=0.49m/s,D点的瞬时速度${v}_{D}=\frac{{x}_{CE}}{2T}=\frac{(23.10-9.81)×1{0}^{-2}}{0.2}$m/s=0.66m/s,
(2)根据△x=aT2,运用逐差法得,a=$\frac{{x}_{DF}-{x}_{BD}}{4{T}^{2}}=\frac{[(31.05-16.02)-(16.02-4.47)]×1{0}^{-2}}{4×0.01}$=0.87m/s2.
故答案为:(1)0.49,0.66.(2)0.87.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.关于麦克斯韦电磁场理论、电磁场和电磁波,下列说法正确的是( )
| A. | 均匀变化的电场周围一定长生均匀变化的磁场 | |
| B. | 变化的电场周围产生磁场,变化的磁场周围产生电场 | |
| C. | 振荡的电场周围产生振荡的磁场,震荡的磁场周围产生震荡电场 | |
| D. | 电磁波的传播需要介质,并且电磁波能发生干涉和衍射现象 |
8. 如图所示为“探究加速度与物体受力及质量的关系”实验装置图.图中A为小车,B为装有砝码的托盘,C为一端带有定滑轮的长木板,小车通过纸带与电火花打点计时器相连,计时器接50Hz交流电.小车的质量为m1,托盘(及砝码)的质量为m2.下列说法正确的是( )
如图所示为“探究加速度与物体受力及质量的关系”实验装置图.图中A为小车,B为装有砝码的托盘,C为一端带有定滑轮的长木板,小车通过纸带与电火花打点计时器相连,计时器接50Hz交流电.小车的质量为m1,托盘(及砝码)的质量为m2.下列说法正确的是( )
 如图所示为“探究加速度与物体受力及质量的关系”实验装置图.图中A为小车,B为装有砝码的托盘,C为一端带有定滑轮的长木板,小车通过纸带与电火花打点计时器相连,计时器接50Hz交流电.小车的质量为m1,托盘(及砝码)的质量为m2.下列说法正确的是( )
如图所示为“探究加速度与物体受力及质量的关系”实验装置图.图中A为小车,B为装有砝码的托盘,C为一端带有定滑轮的长木板,小车通过纸带与电火花打点计时器相连,计时器接50Hz交流电.小车的质量为m1,托盘(及砝码)的质量为m2.下列说法正确的是( )| A. | 每次改变小车质量时,应重新平衡摩擦力 | |
| B. | 实验时应先释放小车后接通电源 | |
| C. | 本实验m2应远大于m1 | |
| D. | 在用图象探究加速度与质量关系时,应作a-$\frac{1}{{m}_{1}}$图象 |
17.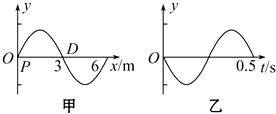 如图所示,一列简谐波在均匀介质中传播,图甲表示t=0时刻的波形图,图乙表示图甲中质点P从t=0时刻开始的振动图象,则这列波( )
如图所示,一列简谐波在均匀介质中传播,图甲表示t=0时刻的波形图,图乙表示图甲中质点P从t=0时刻开始的振动图象,则这列波( )
 如图所示,一列简谐波在均匀介质中传播,图甲表示t=0时刻的波形图,图乙表示图甲中质点P从t=0时刻开始的振动图象,则这列波( )
如图所示,一列简谐波在均匀介质中传播,图甲表示t=0时刻的波形图,图乙表示图甲中质点P从t=0时刻开始的振动图象,则这列波( )| A. | 从左向右传播 | |
| B. | 波的频率为1 Hz | |
| C. | 波速为12 m/s | |
| D. | P质点和D质点在振动过程中同一时刻位移总相同 |
 如图所示,某同学利用光电门传感器探究物体A和B组成的系统在绕过轻滑轮运动时机械能是否守恒的实验,物体A上有宽度为d的遮光条.由静止释放后,A下落,B上升,一段时间后,光电门传感器记录的遮光时间为t.当地的重力加速度为g.为探究该过程中系统的机械能是否守恒,还需要进行一些实验测量和推导.
如图所示,某同学利用光电门传感器探究物体A和B组成的系统在绕过轻滑轮运动时机械能是否守恒的实验,物体A上有宽度为d的遮光条.由静止释放后,A下落,B上升,一段时间后,光电门传感器记录的遮光时间为t.当地的重力加速度为g.为探究该过程中系统的机械能是否守恒,还需要进行一些实验测量和推导.
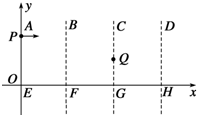 如图所示,竖直平面xOy内有三个宽度均为L首尾相接的电场区域ABFE、BCGF和CDHG.三个区域中分别存在方向为+y、+y、+x的匀强电场,其场强大小比例为2:1:2.现有一带正电的物体以某一初速度从坐标为(0,L)的P点射入ABFE场区,初速度方向水平向右.物体恰从坐标为(2L,$\frac{L}{2}$)的Q点射入CDHG场区,已知物体在ABFE区域所受电场力和所受重力大小相等,重力加速度为g,物体可以视为质点,y轴竖直向上,区域内竖直方向电场足够大.求:
如图所示,竖直平面xOy内有三个宽度均为L首尾相接的电场区域ABFE、BCGF和CDHG.三个区域中分别存在方向为+y、+y、+x的匀强电场,其场强大小比例为2:1:2.现有一带正电的物体以某一初速度从坐标为(0,L)的P点射入ABFE场区,初速度方向水平向右.物体恰从坐标为(2L,$\frac{L}{2}$)的Q点射入CDHG场区,已知物体在ABFE区域所受电场力和所受重力大小相等,重力加速度为g,物体可以视为质点,y轴竖直向上,区域内竖直方向电场足够大.求: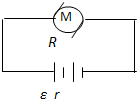 如图所示,一个电源的电动势为E、内电阻为r,将一个电动机接在该电源上,电动机正常工作,通过电动机的电流为I.电动机的内阻为R,关于在时间t内的能量转化,
如图所示,一个电源的电动势为E、内电阻为r,将一个电动机接在该电源上,电动机正常工作,通过电动机的电流为I.电动机的内阻为R,关于在时间t内的能量转化,