题目内容
8．
如图所示，自足够高的同一水平直线上A、B两点相向水平抛出两个小球，两球的初速度分别为v1，v2，运动轨迹如图所示，AO＞BO，不计空气阻力．则下列说法正确的是（ ）| A． | 初速度v1＞v2 | |
| B． | 若两球同时抛出，则两球一定相遇 | |
| C． | 若A先抛出，B后抛出，则两球可能相遇 | |
| D． | 若两球能相遇，则从抛出到相遇的过程中两球的速度变化相同 |
分析 根据下落的高度比较运动的时间，结合水平位移比较初速度．根据时间比较速度的变化量．
解答 解：A、两球相遇时，下落的高度相同，则运动的时间相同，根据x=vt知，v1＞v2，故A正确．
B、因为高度足够高，两球同时从同一高度平抛，相同时间内下落的高度相同，则两球一定相遇．故B正确．
C、因为相遇时，下落的高度相同，运动时间相同，若抛出的先后顺序不同，则两球不会相遇，故C错误．
D、若两球相遇，则运动的时间相同，根据△v=gt知，相遇过程中两球的速度变化量相同，故D正确．
故选：ABD．
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，知道运动的时间由高度决定，初速度和时间共同决定水平位移．
练习册系列答案
相关题目
18．
如图所示的直线是真空中某电场的一条电场线，A、B是这条直线上的两点．一电子以大小为vA的速度经过A点向B点运动，只受电场力的作用，经过一段时间后，电子经过B点是速度的大小为vB，且A、B两处速度方向相反，则（ ）
如图所示的直线是真空中某电场的一条电场线，A、B是这条直线上的两点．一电子以大小为vA的速度经过A点向B点运动，只受电场力的作用，经过一段时间后，电子经过B点是速度的大小为vB，且A、B两处速度方向相反，则（ ）| A． | A点的电势可能低于B点的电势 | |
| B． | A点的场强可能大于B点的场强 | |
| C． | 电子在A点的电势能一定小于它在B点的电势能 | |
| D． | 电子在A点的动能一定小于它在B点的动能 |
19．
如图所示，由A、B两个恒星组成的双星系统，它们在引力作用下绕O点做匀速圆周运动，若A、B两恒星到O点的距离分别为rA和rB，转动的周期为T，引力常量为G，则（ ）
如图所示，由A、B两个恒星组成的双星系统，它们在引力作用下绕O点做匀速圆周运动，若A、B两恒星到O点的距离分别为rA和rB，转动的周期为T，引力常量为G，则（ ）| A． | A恒星的质量可能为$\frac{4{π}^{2}（{r}_{A}+{r}_{B}）^{3}}{G{T}^{2}}$ | |
| B． | 这两颗恒星的角速度之比为$\frac{{ω}_{A}}{{ω}_{B}}$=$\frac{{r}_{B}}{{r}_{A}}$ | |
| C． | 这两颗恒星的向心加速度之比为$\frac{{a}_{A}}{{a}_{B}}$=$\frac{{r}_{B}}{{r}_{A}}$ | |
| D． | 这两颗恒星的线速度之比为$\frac{{v}_{A}}{{v}_{B}}$=$\frac{{r}_{A}}{{r}_{B}}$ |
16．对做下列运动的物体，机械能守恒的是（ ）
| A． | 沿光滑斜面向上的加速度运动的物体 | |
| B． | 在空气阻力不计的条件下，抛出后在空中运动的物体 | |
| C． | 在竖直平面内做匀速圆周运动的物体 | |
| D． | 沿光滑曲面自由下滑的物体 |
如图所示，某同学利用光电门传感器探究物体A和B组成的系统在绕过轻滑轮运动时机械能是否守恒的实验，物体A上有宽度为d的遮光条．由静止释放后，A下落，B上升，一段时间后，光电门传感器记录的遮光时间为t．当地的重力加速度为g．为探究该过程中系统的机械能是否守恒，还需要进行一些实验测量和推导．
20．
两块竖直放置的平行金属板A、B间距为d，两板间电压为U，一质量为m且带正电的质点从两板间的M点开始竖直向上运动，初速度大小为v0，当它到达电场中N点时，速度变为水平方向，大小仍为v0，如图所示，此过程中（忽略带电质点对金属板上电荷均匀分布的影响，重力加速度为g）（ ）
两块竖直放置的平行金属板A、B间距为d，两板间电压为U，一质量为m且带正电的质点从两板间的M点开始竖直向上运动，初速度大小为v0，当它到达电场中N点时，速度变为水平方向，大小仍为v0，如图所示，此过程中（忽略带电质点对金属板上电荷均匀分布的影响，重力加速度为g）（ ）| A． | 质点的机械能守恒 | |
| B． | 电势能的增量为-$\frac{1}{2}$mv${\;}_{0}^{2}$ | |
| C． | M、N两点间的竖直高度差HMN=$\frac{{v}_{0}^{2}}{2g}$ | |
| D． | M、N两点间的电势差UMN=$\frac{U{v}_{0}^{2}}{2dg}$ |
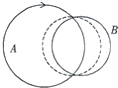如图所示，圆导线环A中通有电流I，方向如图，处于实线位置的圆B的一半面积在A环内，另一半面积在A环外，则圆B内的磁通量不为零（填“为零”、“不为零”），若圆B移至虚线位置，则圆B的磁通量变大（填“变大”、“不变”或“减小”）．
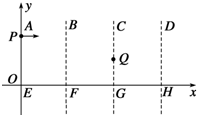如图所示，竖直平面xOy内有三个宽度均为L首尾相接的电场区域ABFE、BCGF和CDHG．三个区域中分别存在方向为+y、+y、+x的匀强电场，其场强大小比例为2：1：2．现有一带正电的物体以某一初速度从坐标为（0，L）的P点射入ABFE场区，初速度方向水平向右．物体恰从坐标为（2L，$\frac{L}{2}$）的Q点射入CDHG场区，已知物体在ABFE区域所受电场力和所受重力大小相等，重力加速度为g，物体可以视为质点，y轴竖直向上，区域内竖直方向电场足够大．求：