题目内容
图中虚线所示为某静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面2的电势为0。一带正电的点电荷在仅受静电力的作用下运动,经过a、b点时的动能分别为12eV和3eV。当这一点电荷运动到某一位置,其电势能变为-5eV时,它的动能应为 ( ) 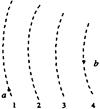
| A.14eV | B.15eV | C.20eV | D.24eV |
A
解析试题分析:设相邻等势面的电势差为U,粒子从a运动到b,电场力做负功,由动能定理得-q×3U=Ekb-Eka,求得U=3V,粒子从1等势面运动到2等势面,由动能定理得-q×U=Ek2-Eka,求得Ek2=9eV。只有电场力做功时,电势能和动能总和不变,粒子在2等势面位置时,电势能与动能总和为9eV,因此当电势能变为-5eV,动能为14eV,A正确。
考点:本题考查动能定理和电场力做功与电势能变化的关系。

 名校课堂系列答案
名校课堂系列答案如图两块平行金属板M、N竖直放置,两板间电势差U=1.5×103 V。现将质量m=1×10-2kg、电荷量q=4×10-5C的带电小球从两板上方的A点以v0=4m/s的初速度水平抛出,小球恰好能从M板上端进入两板之间,并沿直线运动打到N板上的B点.已知A距两板上端的高度为h="0.2" m, 不计空气阻力,g="10" m/s2。则( )
A.小球到达M板上端时的速度大小 |
| B.M、N两板间距d=0.3m |
| C.落点B距N板上端距离L=0.2m |
| D.小球到达B点时动能Ek =0.175J |
如图所示,长为L的轻杆的下端用铰链固接在水平地面上,上端固定一个质量为m的小球,轻杆处于竖直位置,同时与一个质量为M的长方体刚好接触。由于微小扰动,杆向右侧倒下,当小球与长方体分离时,杆与水平面的夹角为30°,且杆对小球的作用力恰好为零,若不计一切摩擦。则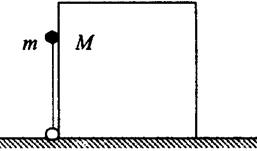
| A.长方体与小球的质量比是4 :1 |
B.分离时小球的速率为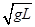 |
C.分离后长方体的速率为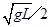 |
| D.长方体对小球做功-mgL/4 |
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知 ( )
| A.三个等势面中,a的电势最高 |
| B.带电质点通过Q点时的加速度较大 |
| C.带电质点通过P点时的动能较大 |
| D.带电质点通过P点时电势能较大 |
图甲是回旋加速器的工作原理图。D1和D2是两个中空的半圆金属盒,它们之间有一定的电势差,A处的粒子源产生的带电粒子,在两盒之间被电场加速。两半圆盒处于与盒面垂直的匀强磁场中,所以粒子在半圆盒中做匀速圆周运动。若带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,不计带电粒子在电场中的加速时间,不考虑由相对论效应带来的影响,下列判断正确的是 
| A.在Ek-t图中应该有tn+1- tn =tn-tn-1 |
| B.在Ek-t图中应该有tn+1- tn <tn-tn-1 |
| C.在Ek-t图中应该有En+1- En =En-En-1 |
| D.在Ek-t图中应该有En+1-En <En-En-1 |
电磁轨道炮工作原理如图所示.待发射弹体可在两平行轨道之间自由移动,并与轨道保持良好接触.电流I从一条轨道流入,通过导电弹体后从另一条轨道流回.轨道电流可形成在弹体处垂直于轨道面的磁场(可视为匀强磁场),磁感应强度的大小与I成正比.通电的弹体在轨道上受到安培力的作用而高速射出.现欲使弹体的出射速度增加至原来的2倍,理论上可采用的办法是( ) 
| A.只将轨道长度L变为原来的2倍 |
| B.只将电流I增加至原来的2倍 |
| C.只将弹体质量减至原来的一半 |
| D.将弹体质量减至原来的一半,轨道长度L变为原来的2倍,其他量不变 |
质量为10kg的物体,在变力F作用下沿x轴做直线运动,力随位移x的变化情况如图所示.物体在x=0处速度为1m/s,一切摩擦不计,则物体运动到x=16m处时,速度大小为( )
A.2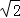 m/s m/s | B.3m/s | C.4m/s | D.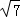 m/s m/s |




