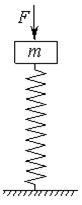
题目内容
如图所示,长为L的轻杆的下端用铰链固接在水平地面上,上端固定一个质量为m的小球,轻杆处于竖直位置,同时与一个质量为M的长方体刚好接触。由于微小扰动,杆向右侧倒下,当小球与长方体分离时,杆与水平面的夹角为30°,且杆对小球的作用力恰好为零,若不计一切摩擦。则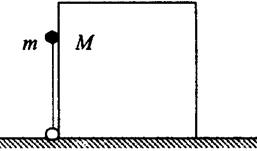
| A.长方体与小球的质量比是4 :1 |
B.分离时小球的速率为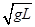 |
C.分离后长方体的速率为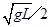 |
| D.长方体对小球做功-mgL/4 |
AD
解析试题分析:在杆从竖直位置开始倒下到小球与长方体恰好分离的过程中,小球和长方体组成的系统机械能守恒,小球和长方体的速度分别为v1和v2,则有: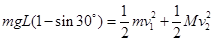 ,分离时刻,小球只受重力,根据向心力公式有:
,分离时刻,小球只受重力,根据向心力公式有: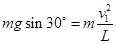 ,此时小球与长方体的水平速度相同,即:
,此时小球与长方体的水平速度相同,即: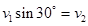 ,联立解得:
,联立解得: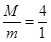 ,故选项A正确;由
,故选项A正确;由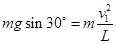 解得:
解得: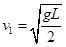 ,
,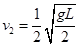 ,故选项BC错误;从小球倾倒到与长方体分离的过程中,对小球由动能定理可知:
,故选项BC错误;从小球倾倒到与长方体分离的过程中,对小球由动能定理可知: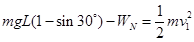 解得:
解得: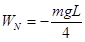 故选项D正确.
故选项D正确.
考点:本题主要考查向心力公式和动能定理的应用,关键是理解“分离”和“杆对小球的作用力为零”的物理意义.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案如图,固定在地面的斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同小球,各球编号如图。斜面与水平轨道OA平滑连接,OA长度为6r。现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦。则在各小球运动过程中,下列说法正确的是( )
| A.球1的机械能守恒 |
| B.球6在OA段机械能增大 |
| C.球6的水平射程最小 |
| D.六个球落地点各不相同 |
如图所示,足够长的传送带以恒定速率顺时针运行。将一个物体轻轻放在传送带底端,第一阶段物体被加速到与传送带具有相同的速度,第二阶段与传送带相对静止,匀速运动到达传送带顶端。下列说法中正确的是 
| A.第一阶段摩擦力对物体做正功,第二阶段摩擦力对物体不做功 |
| B.第一阶段物体和传送带间的摩擦生热等于第一阶段物体重力势能的变化 |
| C.第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加 |
| D.物体从底端到顶端全过程机械能的增加等于全过程摩擦力对物体所做的功 |
如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2分别与质量均为m的小滑块P和小球Q连接。已知光滑直杆两端固定且与两定滑轮在同一竖直平面内,杆与水平面的夹角为θ,直杆上C点与两定滑轮均在同一高度。设直杆足够长,小球运动过程中不会与其他物体相碰。现将小物块从C点由静止释放,在其下滑过程中,下列说法正确的是 ( )
| A.小滑块P的动能先增加后减小 |
| B.小滑块P的机械能先减小后增加 |
| C.小球Q的动能先增加后减小 |
| D.小球Q的机械能先增加后减小 |
图中虚线所示为某静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面2的电势为0。一带正电的点电荷在仅受静电力的作用下运动,经过a、b点时的动能分别为12eV和3eV。当这一点电荷运动到某一位置,其电势能变为-5eV时,它的动能应为 ( ) 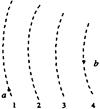
| A.14eV | B.15eV | C.20eV | D.24eV |
如图所示,将一轻弹簧下端固定在倾角为θ的粗糙斜面底端,弹簧处于自然状态时上端位于A点。质量为m的物体从斜面上的B点由静止下滑,与弹簧发生相互作用后,最终停在斜面上。下列说法正确的是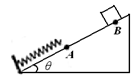
| A.物体最终将停在A点 |
| B.物体第一次反弹后不可能到达B点 |
| C.整个过程中重力势能的减少量大于克服摩擦力做的功 |
| D.整个过程中物体的最大动能小于弹簧的最大弹性势能 |
 、
、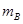 ,且
,且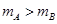 ,置于光滑水平面上,相距较远。将两个大小均为
,置于光滑水平面上,相距较远。将两个大小均为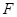 的力,同时分别作用在A、B上经过相同距离后,撤去两个力,两物体发生碰撞并粘在一起后将( )
的力,同时分别作用在A、B上经过相同距离后,撤去两个力,两物体发生碰撞并粘在一起后将( )