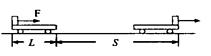题目内容
电磁轨道炮工作原理如图所示.待发射弹体可在两平行轨道之间自由移动,并与轨道保持良好接触.电流I从一条轨道流入,通过导电弹体后从另一条轨道流回.轨道电流可形成在弹体处垂直于轨道面的磁场(可视为匀强磁场),磁感应强度的大小与I成正比.通电的弹体在轨道上受到安培力的作用而高速射出.现欲使弹体的出射速度增加至原来的2倍,理论上可采用的办法是( ) 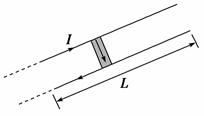
| A.只将轨道长度L变为原来的2倍 |
| B.只将电流I增加至原来的2倍 |
| C.只将弹体质量减至原来的一半 |
| D.将弹体质量减至原来的一半,轨道长度L变为原来的2倍,其他量不变 |
BD
解析试题分析:设两轨道间的距离为l,利用动能定理有 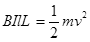 ,B=kI,解得
,B=kI,解得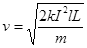 ,若只将轨道长度L变为原来的2倍,弹体的出射速度增加至原来的
,若只将轨道长度L变为原来的2倍,弹体的出射速度增加至原来的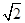 倍,故A错误;只将电流I增加至原来的2倍,弹体的出射速度增加至原来的2倍,故B正确;只将弹体质量减至原来的一半,弹体的出射速度增加至原来的
倍,故A错误;只将电流I增加至原来的2倍,弹体的出射速度增加至原来的2倍,故B正确;只将弹体质量减至原来的一半,弹体的出射速度增加至原来的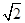 倍,故C错误;将弹体质量减至原来的一半,轨道长度L变为原来的2倍,其它量不变,弹体的出射速度增加至原来的2倍,故D正确.
倍,故C错误;将弹体质量减至原来的一半,轨道长度L变为原来的2倍,其它量不变,弹体的出射速度增加至原来的2倍,故D正确.
考点:本题考查动能定理.

 新题型全程检测期末冲刺100分系列答案
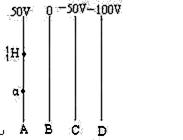
新题型全程检测期末冲刺100分系列答案图中虚线所示为某静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面2的电势为0。一带正电的点电荷在仅受静电力的作用下运动,经过a、b点时的动能分别为12eV和3eV。当这一点电荷运动到某一位置,其电势能变为-5eV时,它的动能应为 ( ) 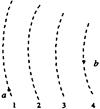
| A.14eV | B.15eV | C.20eV | D.24eV |
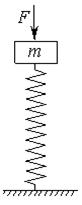
如图所示,将一轻弹簧下端固定在倾角为θ的粗糙斜面底端,弹簧处于自然状态时上端位于A点。质量为m的物体从斜面上的B点由静止下滑,与弹簧发生相互作用后,最终停在斜面上。下列说法正确的是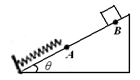
| A.物体最终将停在A点 |
| B.物体第一次反弹后不可能到达B点 |
| C.整个过程中重力势能的减少量大于克服摩擦力做的功 |
| D.整个过程中物体的最大动能小于弹簧的最大弹性势能 |
2013年2月15日中午12时30分左右,俄罗斯车里雅宾斯克州发生陨石坠落事件.这颗陨石进入地球大气层后与空气摩擦而发生剧烈燃烧,并发生爆炸,产生大量碎片.假定某一碎片自爆炸后落至地面并陷入地下一定深度过程中,其质量不变,则
| A.该碎片在空中下落过程中重力做的功等于动能的增加量 |
| B.该碎片在空中下落过程中重力做的功小于动能的增加量 |
| C.该碎片在陷入地下的过程中重力做的功等于动能的改变量 |
| D.该碎片在整个过程中克服阻力的功等于机械能的减少量 |
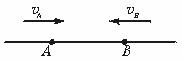
如图所示,竖直放置的两个平行金属板间有匀强电场,在两板之间等高处有两个质量相同的带电小球, P小球从紧靠左极板处由静止开始释放,Q小球从两板正中央由静止开始释放,两小球最后都能打在右极板上的同一点。则从开始释放到打到右极板的过程中( )
A.它们的运行时间 |
B.它们的电荷量之比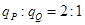 |
C.它们的动能增加量之比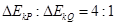 |
D.它们的电势能减少量之比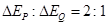 |