题目内容
如图所示，质量均为m、电荷量均为q的带负电的一簇粒子从P1（-a，b）点以相同的速率v0在：xoy平面内朝x轴上方的各个方向射出（即0＜θ≤π），不计重力及粒子间的相互作用，且已知a足够大．
（1）试在图（甲）中的适当位置和区域加一垂直于xoy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动．在图中定性画出所加的最小磁场区域边界的形状和位置．
（2）试在图（乙）中的某些区域加垂直于xoy平面、磁感应强度为B的匀强磁场，使从P1点发出的这簇带电粒子通过磁场后都能通过P2（a，b）点．要求：
①说明所加磁场的方向，并在图中定性画出所加的最小磁场区域边界的形状和位置；
②定性画出沿图示v0方向射出的带电粒子运动的轨迹；
③写出所加磁场区域与xoy平面所成截面边界的轨迹方程．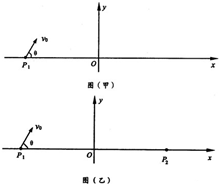
（1）试在图（甲）中的适当位置和区域加一垂直于xoy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动．在图中定性画出所加的最小磁场区域边界的形状和位置．
（2）试在图（乙）中的某些区域加垂直于xoy平面、磁感应强度为B的匀强磁场，使从P1点发出的这簇带电粒子通过磁场后都能通过P2（a，b）点．要求：
①说明所加磁场的方向，并在图中定性画出所加的最小磁场区域边界的形状和位置；
②定性画出沿图示v0方向射出的带电粒子运动的轨迹；
③写出所加磁场区域与xoy平面所成截面边界的轨迹方程．
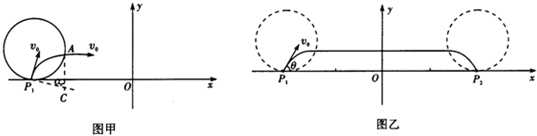
（1）设带电粒子从A点离开磁场区域，A点坐标为（x、y），粒子旋转的半径为R，旋转的圆心在C点，旋转圆心角为α，则
x=一a+Rsinα，
y=R-Rcosα，
解得（x+a）2+（y-R）2=R2．
可见，所加磁场的边界的轨迹是一个以（-a，R）为圆心，
半径为R=
| mv0 |
| Bq |
（2）根据对称性可得出在P2处所加的磁场最小区域也是圆，同理可求得其方程为（x-a）2+（y-R）2=R2
圆心为（a，R），半径为R=
| mv0 |
| Bq |
由数学知识可知该圆位于x轴上方且与P2点相切；
根据左手定则判断得知，磁场方向垂直于xOy平面向里；
沿图示v0方向射出的带电粒子运动的轨迹如图所示．
答：
（1）所加磁场的边界的轨迹是一个以（-a，R）为圆心，半径为R=
| mv0 |
| Bq |
（2）①所加磁场的方向垂直于xOy平面向里；在图中定性画出所加的最小磁场区域边界的形状是圆，该圆位于x轴上方且与P2点相切．如上图所示；
②定性画出沿图示vo方向射出的带电粒子运动的轨迹如图；
③所加磁场区域与xOy平面所成截面边界的轨迹方程为（x-a）2+（y-R）2=R2．圆心为（a，R），半径为R=
| mv0 |
| Bq |
练习册系列答案
相关题目
（2011?河西区二模）如图所示，质量均为m的A、B两球之间系着一根不计质量的弹簧，放在光滑的水平面上，A球紧靠竖直墙壁，今用水平力F将B球向左推压弹簧，平衡后，突然将F撤去，在这瞬间（ ） 
如图所示，质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连，开始时B放在地面上，A、B均处于静止状态，现通过细绳将A缓慢地向上拉起，当B刚要离开地面时，求A上升距离（假设弹簧一直在弹性限度内，重力加速度g已知）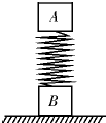
（2013?湖南模拟）如图所示，质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端，当A静止时弹簧的压缩量为l．现用一竖直向下的恒力F=3mg作用于A上，当A运动一段距离x，后撤去F，结果B刚好不离开水平面，则l：x的值为（ ）