题目内容
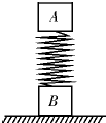（2013?湖南模拟）如图所示，质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端，当A静止时弹簧的压缩量为l．现用一竖直向下的恒力F=3mg作用于A上，当A运动一段距离x，后撤去F，结果B刚好不离开水平面，则l：x的值为（ ）分析：撤去F后，物体B刚好不离开水平面，说明物体B做简谐运动，到最高点时，弹簧对物体B的拉力等于物体B的重力，结合平衡条件求解出物体A的振幅．然后对从开始推物体A到A运动到最高点过程运用动量定理列式求解推论F的作用距离．
解答：解：力F作用前，物体A保持静止，根据平衡条件，有：mg=kl，解得：k=
；
撤去F后，物体B刚好不离开水平面，说明物体B做简谐运动，到最高点时，弹簧对物体B的拉力等于物体B的重力，故kl′=mg，代入k，解得l′=l；
物体A的振幅为2l；
对从力F开始作用到物体A反弹到最高点过程运用动能定理，有：
-mg（2l）+Fx=0-0
（弹簧弹力做功等于弹性势能的变化，为零）
解得：x=
=
=
l；
故l：x=3：2；
故选A．
| mg |
| l |
撤去F后，物体B刚好不离开水平面，说明物体B做简谐运动，到最高点时，弹簧对物体B的拉力等于物体B的重力，故kl′=mg，代入k，解得l′=l；
物体A的振幅为2l；
对从力F开始作用到物体A反弹到最高点过程运用动能定理，有：
-mg（2l）+Fx=0-0
（弹簧弹力做功等于弹性势能的变化，为零）
解得：x=
| 2mgl |
| F |
| 2mgl |
| 3mg |
| 2 |
| 3 |
故l：x=3：2；
故选A．
点评：本题关键对从推论开始作用到物体A反弹到最高点过程采用动能定理列式求解．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
（2013?湖南模拟）如图所示，AB是一段位于竖直平面内的光滑轨道，高度为h，末端B处的切线方向水平．一个质量为m的小物体P从轨道顶端A处由静止释放，滑到B端后飞出，落到地面上的C点，轨迹如图中虚线BC所示，已知它落地时相对于B点的水平位移OC=l．现在轨道下方紧贴B点安装一水平传送带，传送带的右端与B的距离为
（2013?湖南模拟）如图所示，质量为m的物块，沿着半径为R的半球形金属壳内壁滑下，半球形金属壳竖直固定放置，开口向上，滑到最低点时速度大小为v，若物体与球壳之间的摩擦因数为μ，则物体在最低点时，下列说法正确的是（ ）
（2013?湖南模拟）如图所示，从地面上A点发射一枚远程弹道导弹，在引力作用下，沿ACB椭圆轨道飞行击中地面目标B，C为轨道的远地点，距地面高度为h．已知地球半径为R，地球质量为M，引力常量为G．设距地面高度为h的圆轨道上卫星运动周期为T0．则下列结论正确的是（ ）
（2013?湖南模拟）如图所示为一皮带传动装置，右轮的半径为r，a是它边缘上的一点．左侧是一轮轴，大轮的半径为4r，小轮的半径为2r．b点在小轮上，到小轮中心的距离为r．c点和d点分别位于小轮和大轮的边缘上．若在传动过程中，皮带不打滑．则（ ）
（2013?湖南模拟）质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点，随传送带运动到A点后水平抛出，小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑的圆孤轨道下滑．B、C为圆弧的两端点，其连线水平．已知圆弧半径R=1.0m圆弧对应圆心角θ=106°，轨道最低点为O，A点距水平面的高度h=0.8m，小物块离开C点后恰能无碰撞的沿固定斜面向上运动，0.8s后经过D点，物块与斜面间的动摩擦因数为μ1=