题目内容
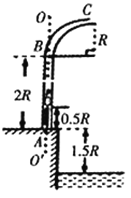
【题目】如图为某种鱼饵自动投放器的装置示意图,其下部AB是一长为2R的竖直细管,上部BC是半径为R的四分之一圆弧弯管管口,C处切线水平,AB管内有原长为R、下端固定的轻质弹簧,在弹簧上端放置一粒质量为m,可视为质点的鱼饵解除锁定后弹簧可将鱼饵弹射出去。投饵时,每次总将弹簧长度压缩到0.5R后锁定,此时弹簧的弹性势能为8mgR(g为重力加速度),不计鱼饵在运动过程中的机械能损失,重力加速度为g,求:
(1)鱼饵到达管口C时的速度大小v1;
(2)鱼饵到达管口C时对管子的作用力大小和方向;
(3)已知地面比水面高出1.5R,若竖直细管的长度可以调节,圆弧弯道管BC可随竖直细管一起升降,求鱼饵到达水面的落点与AB所在竖直线OO′之间的最大距离Lmax。
【答案】(1)![]() ;(2)10mg,竖直向上;(3)11R
;(2)10mg,竖直向上;(3)11R
【解析】
(1)鱼饵到达管口C的过程中,机械能守恒,有:
![]()
解得: v1=![]()
(2)设在C处管子对鱼饵的作用下向下,大小为FN,由牛顿第二定律可得:
![]()
解得:![]()
根椐牛顿第三定律可得鱼饵对管子的作用力为10mg,方向竖直向上.
(3)设AB长度为h,对应平抛水平距离为x,由机械能守恒定律可得:
![]()
鱼饵从管口C做平抛运动,则
水平方向:![]()
竖直方向:![]()
联立解得:![]()
当h=2.5R时,x有最大值为![]()
则![]()
![]()

练习册系列答案
相关题目