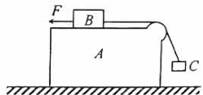
题目内容
 水平面上有带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的.用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图,已知物体A、B、C的质量均为m,重力加速度为g,不计所有的摩擦,求:
水平面上有带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的.用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图,已知物体A、B、C的质量均为m,重力加速度为g,不计所有的摩擦,求:(1)BC间绳拉力T表达式(用mg表示)
(2)系统的加速度;
(3)F应为多大?(用mg表示)
分析:本题为连接体类问题,应分别研究整体、物体B及物体C,由牛顿第二律列出表达式联立可求得加速度,则由整体法可求得拉力F.
解答:解:(1)设绳中张力为T,A、B、C共同的加速度为a,与C相连部分的绳与竖直线夹角为α,由牛顿运动定律,对A、B、C 组成的整体有:
F=3ma …①
对B有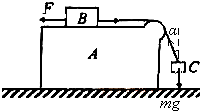 :
:
F-T=ma …②
对C有:
Tcosα=mg …③
Tsinα=ma …④
联立①②式得:
T=2ma …⑤
联立③④式得:
T2=m2(g2+a2)…⑥
联立⑤⑥式得:
a=
g…⑦
T=
mg
利用①⑦式得:
F=
mg
答:(1)BC间绳拉力T表达式为
mg;
(2)系统的加速度为=
g;
(3)F应为
mg.
F=3ma …①
对B有
 :
:F-T=ma …②
对C有:
Tcosα=mg …③
Tsinα=ma …④
联立①②式得:
T=2ma …⑤
联立③④式得:
T2=m2(g2+a2)…⑥
联立⑤⑥式得:
a=
| ||
| 3 |
T=
2
| ||
| 3 |
利用①⑦式得:
F=
| 3 |
答:(1)BC间绳拉力T表达式为
2
| ||
| 3 |
(2)系统的加速度为=
| ||
| 3 |
(3)F应为
| 3 |
点评:连接体的处理方法就是要灵活应用整体法与隔离法,正确选择研究对象可以起到事半功倍的效果;本题在对C的分析中,要注意C竖直方向受力平衡,而水平方向具有水平向左的加速度.

练习册系列答案
相关题目
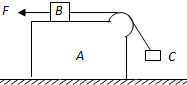
 (2008?四川)水平面上有一带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的.用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图.已知物体A、B、C、的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应为多大?
(2008?四川)水平面上有一带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的.用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图.已知物体A、B、C、的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应为多大? 水平面上有一带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的。用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止。如图,已知物体A、B、C的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应多大?
水平面上有一带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的。用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止。如图,已知物体A、B、C的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应多大?