题目内容
15.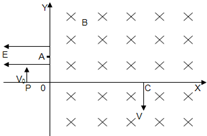 如图所示,在直角坐标xoy平面的第二象限内存在水平向左、电场强度为E的匀强电场,在第一象限和第四象限内存在垂直纸面向里的匀强磁场,一质量为m,电荷量为e的电子,从x轴上的P点以初速度v0沿Y轴正方向进入第二象限内的匀强电场中,并从Y轴上的A点进入第第一象限内的匀强磁场做圆周运动,之后其沿y轴负方向从x轴上的C点射入第四象限.已知v0=$\sqrt{\frac{2eEL}{m}}$,P的坐标为(-L,0).
如图所示,在直角坐标xoy平面的第二象限内存在水平向左、电场强度为E的匀强电场,在第一象限和第四象限内存在垂直纸面向里的匀强磁场,一质量为m,电荷量为e的电子,从x轴上的P点以初速度v0沿Y轴正方向进入第二象限内的匀强电场中,并从Y轴上的A点进入第第一象限内的匀强磁场做圆周运动,之后其沿y轴负方向从x轴上的C点射入第四象限.已知v0=$\sqrt{\frac{2eEL}{m}}$,P的坐标为(-L,0).(1)若L=1m,其余各物理量均未知,求A点的坐标.
(2)电子经过A点时的速度方向与Y轴正方向的夹角θ.
(3)若$\sqrt{\frac{mE}{eL}}$=1T,其余各物理量均未知,求磁场的磁感应强度B.
分析 (1)电子在电场中做类平抛运动,应用类平抛运动规律可以求出A点的坐标.
(2)电子在电场中做类平抛运动,应用类平抛运动可以求出电子的速度方向与Y轴正方向间的夹角.
(3)电子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出磁感应强度.
解答 解:(1)电子在电场中做类平抛运动: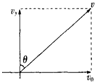
水平方向:L=v0t
竖直方向:y=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{eE}{m}$t2,
已知:L=1m,
解得:y=2L=2m,A点坐标为:(0,2m).
(2)电子在电场中做类平抛运动:
水平方向:L=v0t
竖直方向:vy=at=$\frac{eE}{m}$t,
tanθ=$\frac{{v}_{0}}{{v}_{y}}$,
解得:tanθ=1,则:θ=45°;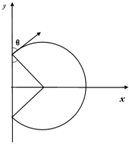
(3)电子在磁场中做匀速圆周运动,运动轨迹如图所示:
由牛顿第二定律得:evB=m$\frac{{v}^{2}}{r}$,
由图中几何关系可知:r=$\frac{2L}{sinθ}$=2$\sqrt{2}$L,
已知:$\sqrt{\frac{mE}{eL}}$=1T,
解得:B=$\frac{\sqrt{2}}{2}$T;
答:(1)若L=1m,其余各物理量均未知,A点的坐标为:(0,2m).
(2)电子经过A点时的速度方向与Y轴正方向的夹角θ为45°.
(3)若$\sqrt{\frac{mE}{eL}}$=1T,其余各物理量均未知,磁场的磁感应强度B为$\frac{{\sqrt{2}}}{2}T$.
点评 本题考查了电子在电场与磁场中的运动问题,是电磁学与力学的一道综合题,分析清楚电子的运动过程,应用类平抛运动规律、运动的合成与分解、牛顿第二定律、运动学公式即可正确解题.

练习册系列答案
相关题目
6.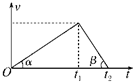 用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )
用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )
 用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )
用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )| A. | W=W1+W2 | B. | P<P1+P2 | C. | W1=W2 | D. | P1>P2 |
3. 左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )
左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )
 左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )
左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )| A. | C1用大电容,C2用大电容 | B. | C1用大电容,C2用小电容 | ||
| C. | C1用小电容,C2用大电容 | D. | C1用小电容,C2用小电容 |
7.水滴自高处由静止开始下落,至落地前的过程中遇到水平方向吹来的风,则( )
| A. | 风速越大,水滴落地时的瞬时速度越大 | |
| B. | 风速越大,水滴下落的时间越长 | |
| C. | 水滴下落的时间与风速无关 | |
| D. | 水滴着地时的瞬时速度与风速无关 |
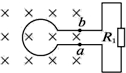 如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=0.2tT,定值电阻R1=6Ω,线圈电阻R2=4Ω.求:
如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=0.2tT,定值电阻R1=6Ω,线圈电阻R2=4Ω.求: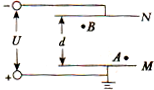 如图,平板电容器d=1.2cm,U=240V,M板接地,AM距离0.2cm,BN距离0.5cm,一个q=-3×10-4C的电荷放在A处,试求:
如图,平板电容器d=1.2cm,U=240V,M板接地,AM距离0.2cm,BN距离0.5cm,一个q=-3×10-4C的电荷放在A处,试求: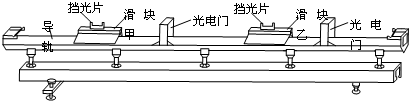
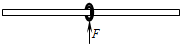 如图所示,一个质量为m的钢性圆环套在一根固定的足够长的水平直杆上,环的半径略大于杆的半径.环与杆之间的动摩擦因数为μ,t=0时刻给环一个向右的初速度v0,同时对环施加一个方向始终竖直向上的力F,已知力F的大小F=kv(k为常数,v为环的运动速度),且有kv0>mg.t=t1时刻环开始沿杆做匀速直线运动,试求:
如图所示,一个质量为m的钢性圆环套在一根固定的足够长的水平直杆上,环的半径略大于杆的半径.环与杆之间的动摩擦因数为μ,t=0时刻给环一个向右的初速度v0,同时对环施加一个方向始终竖直向上的力F,已知力F的大小F=kv(k为常数,v为环的运动速度),且有kv0>mg.t=t1时刻环开始沿杆做匀速直线运动,试求: