题目内容
20.气垫导轨在现在的中学物理实验中应用很广泛,如图所示为一种简单的气垫导轨.导轨上的甲、乙两滑块质量分别为m1、m 2,且m1>m2,两滑块上的挡片宽度相同,均为L.现将气垫导轨水平放置做“验证动量守恒定律”实验.实验中用滑块甲撞击静止在导轨上的滑块乙,碰撞前滑块乙处于静止状态.第一次在两滑块碰撞端安上弹簧片,第二次在两滑块碰撞端粘上橡皮泥,弹簧片与橡皮泥的质量均不计.两次实验时滑块甲碰前通过光电门计时装置记录的挡光片的挡光时间相等,均为t,碰后滑块乙第一次和第二次通过光电门计时装置记录的挡片挡光时间分别为t1、t2,则(光电门的宽度可忽略)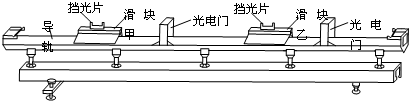
(1)通过所给数据验证动量守恒定律的表达式为m1$\frac{L}{t}$=(m1+m2)$\frac{l}{{t}_{2}}$.上式中算得的甲、乙两滑块的动量大小并不完全相等,产生误差的原因是①存在阻力②导轨不水平(写出两点即可).
(2)t1和t2的关系应为t1<t2.(选填“>”“<”“=”)
(3)滑块甲第一次与乙碰撞后通过光电门的时间t′=$\frac{{m}_{1}t{t}_{1}}{{m}_{1}{t}_{1}-{m}_{2}t}$.(用所给的数据表示)
分析 (1)根据动量守恒表达式可求得动量守恒的表达式;(2)再根据弹性碰撞与非弹性碰撞的特点分析两次滑块获得的速度大小,进而分析所需时间长短.
(3)根据动量守恒定律求得碰后甲的速度,再由速度公式可求得通过光电门的时间.
解答 解:(1)碰前甲的速度均为:v0=$\frac{L}{t}$;碰后甲乙速度相同,v2=$\frac{l}{{t}_{2}}$
则应验证的表达式为:m1$\frac{L}{t}$=(m1+m2)$\frac{l}{{t}_{2}}$;
得出的动量并不完全相等的原因主要是由于外力的存在导致动量并不守恒;如①空气阻力②导轨不水平等;
(2)碰后甲的速度第一次装上弹簧片,所以没有机械能的损失,则交换速度,第二次碰撞过程中机械能损失较大,所以乙获得的速度较小,则第一次通过光电门所用时间短,即t1<t2;
(3)对于第一次碰撞由动量守恒定律可知:
m1$\frac{l}{t}$=m1$\frac{l}{t′}$+m2$\frac{l}{{t}_{1}}$
解得:t′=$\frac{{m}_{1}t{t}_{1}}{{m}_{1}{t}_{1}-{m}_{2}t}$
故答案为:(1)m1$\frac{L}{t}$=(m1+m2)$\frac{l}{{t}_{2}}$;①存在阻力②导轨不水平;
(2)<
(3)$\frac{{m}_{1}t{t}_{1}}{{m}_{1}{t}_{1}-{m}_{2}t}$
点评 本题考查了弹性碰撞与非弹性碰撞的区别与特点,弹性碰撞中没有机械能损失.
要掌握实验注意事项、明确用光电门表示瞬时速度的方法.

练习册系列答案
相关题目
11.以下是有关热学内容的若干叙述,其中正确的是( )
| A. | 布朗运动虽然不是液体分子的运动,但是它可以说明分子在永不停息地做无规则运动 | |
| B. | 给自行车轮胎打气,越来越费力,主要是由于打气过程中分子间斥力逐渐增大,引力逐渐减小的缘故 | |
| C. | 系统的熵只能增大或不变,不可能减小 | |
| D. | 通常情况下,一定质量的理想气体在等温膨胀的过程中,既不吸热,也不放热 | |
| E. | 非晶体的结构跟液体非常类似,可以看作是粘滞性极大的液体 | |
| F. | 所有的金属在常温下都呈固态 | |
| G. | 液体表面层的分子比液体内部的分子有更大的分子势能 | |
| H. | 由热力学第二定律可以判断物理过程能否自发进行 |
5.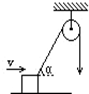 如图所示,木块在水平桌面上移动的速度是v,跨过滑轮的绳子向下移动的速度是(绳与水平方向之间的夹角为α)( )
如图所示,木块在水平桌面上移动的速度是v,跨过滑轮的绳子向下移动的速度是(绳与水平方向之间的夹角为α)( )
 如图所示,木块在水平桌面上移动的速度是v,跨过滑轮的绳子向下移动的速度是(绳与水平方向之间的夹角为α)( )
如图所示,木块在水平桌面上移动的速度是v,跨过滑轮的绳子向下移动的速度是(绳与水平方向之间的夹角为α)( )| A. | v | B. | vcosα | C. | vsinα | D. | vtanα |
9.关于平抛运动,下列说法不正确的是( )
| A. | 平抛运动是匀变速运动 | B. | 平抛运动是变加速运动 | ||
| C. | 任意两段时间内加速度相同 | D. | 任意两段相等时间内速度变化相同 |
10.下列说法正确的是( )
| A. | 在任何电场的周围空间一定存在磁场 | |
| B. | 只有温度超过零度的物体才能向外发射红外线 | |
| C. | 变化的电场和磁场相互激发,由近及远传播形成电磁波 | |
| D. | 电磁波和声波一样传播都需要介质 |
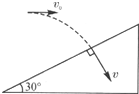 如图所示,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞击在倾角θ=30°的斜面上,求:
如图所示,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞击在倾角θ=30°的斜面上,求: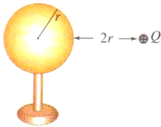 一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧有一个+Q的点电荷,距金属球边缘最近距离为2r,则感应电荷在球心激发的场强大小为k$\frac{Q}{9{r}^{2}}$,方向向右(向左或向右)
一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧有一个+Q的点电荷,距金属球边缘最近距离为2r,则感应电荷在球心激发的场强大小为k$\frac{Q}{9{r}^{2}}$,方向向右(向左或向右)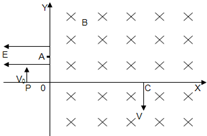 如图所示,在直角坐标xoy平面的第二象限内存在水平向左、电场强度为E的匀强电场,在第一象限和第四象限内存在垂直纸面向里的匀强磁场,一质量为m,电荷量为e的电子,从x轴上的P点以初速度v0沿Y轴正方向进入第二象限内的匀强电场中,并从Y轴上的A点进入第第一象限内的匀强磁场做圆周运动,之后其沿y轴负方向从x轴上的C点射入第四象限.已知v0=$\sqrt{\frac{2eEL}{m}}$,P的坐标为(-L,0).
如图所示,在直角坐标xoy平面的第二象限内存在水平向左、电场强度为E的匀强电场,在第一象限和第四象限内存在垂直纸面向里的匀强磁场,一质量为m,电荷量为e的电子,从x轴上的P点以初速度v0沿Y轴正方向进入第二象限内的匀强电场中,并从Y轴上的A点进入第第一象限内的匀强磁场做圆周运动,之后其沿y轴负方向从x轴上的C点射入第四象限.已知v0=$\sqrt{\frac{2eEL}{m}}$,P的坐标为(-L,0).