题目内容
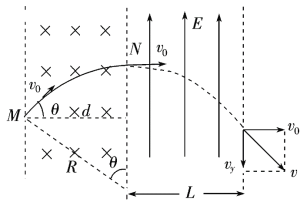
【题目】如图所示，带电粒子以某一初速度进入一垂直于纸面向里、磁感应强度为B的有界匀强磁场，粒子垂直进入磁场时的速度与水平方向成θ＝
角，接着垂直进入电场强度大小为E，水平宽度为L、方向竖直向上的匀强电场，粒子穿出电场时速度大小变为原来的
倍，已知带电粒子的质量为m、电荷量为q，重力不计。
(1)分析判断粒子的电性;
(2)求带电粒子在磁场中运动时速度v;
(3)求磁场的水平宽度d.
【答案】（1）带负电 （2）v0＝ 
（3）
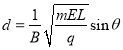
【解析】
(1)根据粒子在磁场中向下偏转的情况和左手定则可知，粒子带负电；
(2)由于洛伦兹力对粒子不做功，故粒子以原来的速率进入电场中，设带电粒子进入电场的初速度为v0，在电场中偏转时做类平抛运动，如图所示．由题意知粒子离开电场时的末速度大小为v＝
，将vt分解为平行于电场方向和垂直于电场方向的两个分速度：由几何关系知
vy＝v0
由运动学公式：
vy＝at
L＝v0t
根据牛顿第二定律：
a＝
＝
联立解得：
v0＝
(3)如图所示，带电粒子在磁场中所受洛伦兹力作为向心力，设在磁场中做圆周运动的半径为R，则：
qv0B＝m
由几何知识可得：
d＝Rsinθ
联立解得：
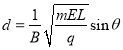
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
