题目内容
【题目】如图所示,开口向上、粗细均匀的玻璃管竖直放置,管内用两段水银柱封闭了两部分理想气体,AB段和CD段分别是两段长h=15 cm的水银柱。BC段气柱长l1=5 cm, D到玻璃管底端长l2=5 cm。已知大气压强是75 cmHg,玻璃管的导热性能良好,环境的温度T0=300 K,以下过程中水银均未从管内流出。
①将玻璃管从足够高处由静止释放,不计空气阻力,求下落过程中A处的水银面沿玻璃管移动的距离xA;
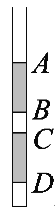
②保持玻璃管静止,缓慢升高环境温度,同样可以使A处的水银面沿玻璃管移动到与①中所求相同的位置,求此时环境温度T。
【答案】①3 cm ②T=390K
【解析】
①静止时,BC段气体的压强为p1 =75 cmHg+15 cmHg=90 cmHg
D到玻璃管底端气体的压强为p2=75 cmHg+15 cmHg+15 cmHg=105 cmHg
自由下落后,水银柱产生的压强消失,上下两部分气体的压强均为p0=75 cmHg
根据玻意耳定律得,
p1l1=p′1l′1
p2l2=p′2l′2
解得
l′1=6 cm
l′2=7cm
xA=l′1+l′2-l1-l2=3 cm
②缓慢升高环境温度的过程中,上下两部分气体均做等压变化,由盖·吕萨克定律得
![]() =
=![]()
![]() =
=![]()
由于l1=l2,xA=3 cm,故最终
l″1=l″2=6.5 cm
解得
T=390 K

练习册系列答案
相关题目