Question

【题目】如图所示，一足够长斜面倾角θ=37°，斜面上有一质量为m=1kg的木板，在木板上放一质量也为m=1kg的金属块（可看成质点），t=0时刻金属块的速度为v0=20m/s。方向沿斜面向上，同时给木板施加一个眼斜面向上的拉力F=14N，使木板从静止开始运动。当t=2s时撤去拉力F，已知金属块和木板间动摩擦因数μ1=0.25，木板和斜面间动摩擦因数μ2=0.5，最大静摩擦力等于滑动摩擦力，求：

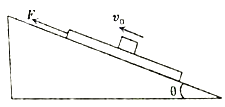
（1）前2s内金属块和木板的加速度；

（2）从t=0到金属块速度减小到0的过程中木板在斜面上的位移（此过程金属块始终未离开木板，计算结果保留三位有效数字）。

Answer 1

【答案】(1) 金属块的加速度，方向沿斜面向下，木板的加速度，方向沿斜面向上 (2)

【解析】

(1)对金属块和木板应用牛顿运动定律有

解得金属块的加速度，方向沿斜面向下，

木板的加速度，方向沿斜面向上。

(3)2s末金属块的速度为，

木板的速度为

可见撤去F时金属块和木板速度相等。

分析得知此后一段时间金属块的加速度仍为，方向沿斜面向下。

设此后一段时间板的加速度为：

由牛顿第二定律可得：，

解得，方向沿斜面向下。

由于，故木板速度先减到零，此后在金属块上滑的过程中，假设木板静止在斜面上斜面上，受到斜面的静摩擦力为f，则，f=4N

木板和斜面之间的最大静摩擦力,，假设成立。

设金属块速度减小到0,的过程中木板在斜面上滑动的位移为x，则，方向沿斜面向上。