��Ŀ����
����Ŀ����ͼ��ʾ���⻬��![]() ��O�˹̶�һ����ϵ��Ϊ
��O�˹̶�һ����ϵ��Ϊ![]() ��ԭ��Ϊ
��ԭ��Ϊ![]() �����ʵ��ɣ�����Ϊm=1kg��С�����ڹ⻬���ϲ��뵯�ɵ��϶����ӡ�
�����ʵ��ɣ�����Ϊm=1kg��С�����ڹ⻬���ϲ��뵯�ɵ��϶����ӡ�![]() Ϊ��O�����ֱ�ᣬ����ˮƽ���ļн�ʼ��Ϊ
Ϊ��O�����ֱ�ᣬ����ˮƽ���ļн�ʼ��Ϊ![]() ����ʼ�˴��ھ�ֹ״̬��������
����ʼ�˴��ھ�ֹ״̬��������![]() Ϊ��ת��ʱ�����ٶȴ��㿪ʼ�������ӣ�ֱ�������쳤��Ϊ0.5m���������ٶ�gȡ
Ϊ��ת��ʱ�����ٶȴ��㿪ʼ�������ӣ�ֱ�������쳤��Ϊ0.5m���������ٶ�gȡ![]() ������˵����ȷ����( )
������˵����ȷ����( )

A. �����ɻָ�ԭ��ʱ����ת���Ľ��ٶ�Ϊ![]()
B. �����ɵ��쳤��Ϊ0.5mʱ����ת���Ľ��ٶ�Ϊ![]()
C. �ڴ˹����У�С��͵�����ɵ�ϵͳ��е���غ�
D. �ڴ˹����У��˶�С������Ϊ12.5J
���𰸡�BD
��������A�������ɻָ�ԭ��ʱ������������֧�����������ṩ����������ţ�ٵڶ����ɿɵã� ![]() ����ã�
����ã� ![]() ����A����
����A����
B���������쳤��Ϊ![]() ʱ��С��������ͼʾ��
ʱ��С��������ͼʾ��
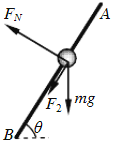
ˮƽ�����ϣ� ![]()
��ֱ�����ϣ� ![]()
���ɵĵ���Ϊ�� ![]()
������ã� ![]() ����B��ȷ��
����B��ȷ��
C���ڴ˹����У��˵ĵ�������͵���ϵͳ���������ʻ�е�ܲ��غ㣬��C����
D���ڴ˹����У��ɶ��ܶ����ɵã� ![]() ����ã�
����ã� ![]() ����D��ȷ��
����D��ȷ��

��ϰ��ϵ�д�
�����Ŀ