题目内容
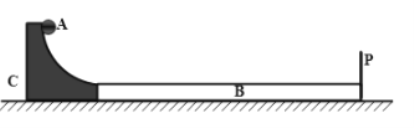
【题目】如图所示,ab是以O为圆心、半径R=2.6m的一段光滑圆弧轨道,轨道固定在竖直平面内且与粗糙水平地面相切于b点。质量m2=1kg的长木板B静止在地面上,木板左端与b点的水平距离s=1m,木板右端上表面放有质量m3=1kg、可视为质点的物块C。让质量m1=0.5kg的小物块A以一定的初速度沿轨道ab下滑,当A即将经过b点时受到轨道的支持力大小等于A所受重力的5倍,之后A与木板发生正碰,碰后A恰好返回到b点停止运动。已知物块C与木板间的动摩擦因数1=0.1,物块A、木板与地面间的动摩擦因数均为2=0.2,最大静摩擦力等于滑动摩擦力,整个过程物块C始终在木板上。取g=10m/s2。求:
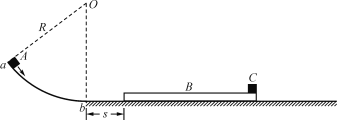
(1)物块A与木板碰撞过程中系统损失的机械能;
(2)物块C最终停在距离木板右端多远的地方?
【答案】(1)6J(2)2.67m处
【解析】
(1)设A经过b点时的速度大小为v0,由牛顿第二定律得![]()
依题意 FN = 5m1g
设A与木板相碰前、后的速度大小分别为v1、v1,碰后木板的速度大小为v2,由动量守恒定律有m1v1 = m1v1 + m2v2
A沿地面向右滑行过程,由动能定理得2m1gs =![]() m1v12
m1v12 ![]() m1v02
m1v02
A与木板碰后返回的过程,由动能定理得2m1gs = 0 ![]() m1v12
m1v12
联立以上各式并代入数据解得v1 = 10m/s,v1 = 2m/s,v2 = 6m/s
系统碰撞过程中损失的机械能![]()
代入数据解得 ΔE = 6J
(2)碰后木板B减速运动,物块C加速运动,设B、C达到共同速度之前加速度大小分别为a1、a2,由牛顿第二定律
对木板有 ![]()
对物块C有 ![]()
设经历时间t后B、C达到共同速度v,则有v = v2 a1t,v = a2t
这一过程中C相对B向左的位移大小为![]()
联立以上各式并代入数据解得 Δx1 = 3m
B、C达到共同速度之后,因![]() ,二者将各自减速至停止,设B、C的加速度大小分别为a3、a4,由牛顿第二定律
,二者将各自减速至停止,设B、C的加速度大小分别为a3、a4,由牛顿第二定律
对木板有 ![]()
对物块C有 ![]()
这一过程中C相对B向右的位移大小为![]()
联立以上各式并代入数据解得 ![]()
整个过程中C相对B向左的位移大小为![]()
![]() m = 2.67m
m = 2.67m
所以物块C最终停在距离木板右端2.67m处。

【题目】在“用DIS研究在温度不变时,一定质量的气体压强与体积的关系”实验中,某同学将注射器活塞置于刻度为10mL处,然后将注射器连接压强传感器并开始实验,气体体积V每增加1mL测一次压强p,最后得到p和V的乘积逐渐增大。
(1)由此可推断,该同学的实验结果可能为图__________。
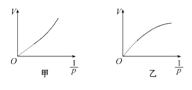
(2)图线弯曲的可能原因是在实验过程中( )
A.注射器中有异物 | B.连接软管中存在气体 |
C.注射器内气体温度升高 | D.注射器内气体温度降低 |