题目内容
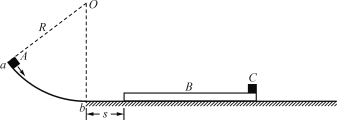
【题目】如图所示，水平地面上左侧有一质量为2m的四分之一光滑圆弧斜槽C，斜槽末端切线水平，右侧有一质量为3m的带挡板P的木板B，木板上表面水平且光滑，木板与地面的动摩擦因数为0.25，斜槽末端和木板左端平滑过渡但不粘连。某时刻，一质量为m的可视为质点的光滑小球A从斜槽顶端静止滚下，重力加速度为g，求:
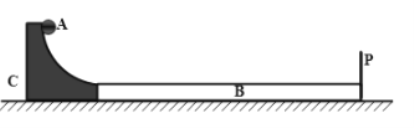
(1)若光滑圆弧斜槽C不固定，圆弧半径为R且不计斜槽C与地面的摩擦，求小球滚动到斜槽末端时斜槽的动能?
(2)若斜槽C固定在地面上，小球从斜槽末端滚上木板左端时的速度为v0，小球滚上木板的同时，外界给木板施加大小为v0的水平向右初速度，并且同时分别在小球上和木板上施加水平向右的恒力F1与F2，且F1=F2=0.5mg。当小球运动到木板右端时(与挡板碰前的瞬间)，木板的速度刚好减为零，之后小球与木板的挡板发生第1次相碰，以后会发生多次碰撞。已知小球与挡板都是弹性碰撞且碰撞时间极短，小球始终在木板上运动。求:
①小球与挡板第1次碰撞后的瞬间，木板的速度大小。
②小球与挡板第1次碰撞后至第10次碰撞后瞬间的过程中F1与F2做功之和。
【答案】（1）
（2）①2v0②
【解析】
（1）由题可知，设小球滚到斜槽末端时，A与C的速度大小分别为vA、vC。A与C系统水平方向动量守恒，取水平向右为正方向，则
A与C系统的机械能守恒，则
小球滚动到斜槽末端时斜槽的动能
解得
（2）①小球滚到木板上后，小球与木板的加速度大小分别为a1和a2。则
木板开始运动到速度第一减为零的时间为
小球第一次与挡板碰撞前瞬间的速度为
另设小球与挡板第1次碰撞后的瞬间，小球与木板的速度分别为vA1、vB1，取向右为正方向，A与B动量守恒，则得
A与B系统的总动能不变，则
解得
vA1=-2v0，vB1=2v0
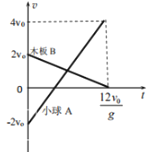
②由题可知，第1次碰撞后，小球以2v0沿木板向左匀减速运动再反向匀加速，木板以2v0向右匀减速运动（两者v-t图象如图所示），木板速度再次减为零的时间
小球的速度
此时，小球的位移
木板的位移
即小球、木板第2次相碰前瞬间的速度与第1次相碰前瞬间的速度相同，以后小球、木板重复前面的运动过程。则第1次碰撞后与第10次碰撞后瞬间，小球与木板总位移相同，都为
由此过程F1与F2做功之和
解得
答：（1）（2）①2v0②
名校名卷单元同步训练测试题系列答案
