Question

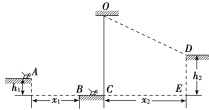
【题目】山谷中有三块石头和一根不可伸长的轻质青藤，其示意图如下．图中A、B、C、D均为石头的边缘点，O为青藤的固定点，h1＝1．8 m，h2＝4．0 m，x1＝4．8 m，x2＝8．0 m．开始时，质量分别为M＝10 kg和m＝2 kg的大、小两只滇金丝猴分别位于左边和中间的石头上，当大猴发现小猴将受到伤害时，迅速从左边石头的A点水平跳至中间石头．大猴抱起小猴跑到C点，抓住青藤下端，荡到右边石头上的D点，此时速度恰好为零．运动过程中猴子均可看成质点，空气阻力不计，重力加速度g取10 m/s2．求：

（1）大猴从A点水平跳离时速度的最小值；

（2）猴子抓住青藤荡起时的速度大小；

（3）猴子荡起时，青藤对猴子的拉力大小．

Answer 1

【答案】（1）8 m/s （2）9 m/s （3）216 N

【解析】

试题分析：（1）设猴子从A点水平跳离时速度的最小值为vmin，根据平抛运动规律，有

h1＝gt2①

x1＝vmint②

联立①②式，得

vmin＝8 m/s③

（2）猴子抓住青藤后的运动过程中机械能守恒，设荡起时速度为vC，有

（M＋m）gh2＝（M＋m）v④

vC＝＝ m/s≈9 m/s⑤

（3）设拉力为FT，青藤的长度为L，对最低点，由牛顿第二定律得

FT－（M＋m）g＝（M＋m）⑥

由几何关系

（L－h2）2＋x＝L2⑦

得：L＝10 m⑧

综合⑤⑥⑧式并代入数据解得：

FT＝（M＋m）g＋（M＋m）＝216 N．