题目内容
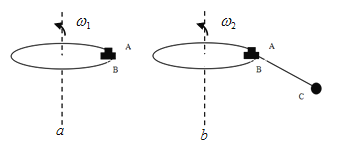
【题目】如图所示，在水平转台上开有一小孔O，一根轻绳穿过小孔，一端拴一质量为1kg的物体A，另一端连接质量为0.5kg的物体B。已知O与A间的距离r为10cm，A与转台的滑动摩擦因数μ为0.1（设最大静摩擦力等于滑动摩擦力），转台从静止开始缓慢加速转动，开始时绳子拉直但张力为0，且物体A（可视为质点）始终与转台相对静止， 
（1）当转台角速度
为多少时绳子开始由拉力？
（2）当转台角速度
时，B对地面的压力
？
（3）要使物体B离开地面，则转台旋转的角速度
至少为多大？
【答案】（1）
（2）
（3）
【解析】（1）当物体A与平台之间的最大摩擦力恰好提供向心力时，根据牛顿第二定律： 
，解得： 
。
（2）当转台角速度
时，对物体A，根据牛顿第二定律： 
，解得： 
，方向指向圆心，以B为研究对象，B受到重力．绳子的拉力和地面的支持力处于平衡状态，则： 
，所以： 
根据牛顿第三定律可知，B对地面的压力
也是
；
（3）要使物B离开地面，则绳子对B的拉力等于B的重力，即： 
对A，则： 
，代入数据得： 
。
练习册系列答案
相关题目
